こんにちは、リブセンスで統計や機械学習関係の仕事をしている北原です。今回は階層ベイズを使った小技の紹介です。推定にはStanを使います。
Webサービスに限らないかもしれませんが、CVRやCTRなど比率データを扱うことって多いですよね。弊社の求人サービスは成果報酬型であるため、各求人の採用率などを知りたいこともよくあります。しかし、求人別だとバイト求人や転職求人の応募数はそれほど多くないので、採用数を応募数で単純に割っただけでは極端な採用率になりがちです。今回は、このような分母の値が小さい比率のデータを、階層ベイズを使って計算する方法を紹介します。
応募数が少ないときの採用率計算の問題
まず、応募数が少ない求人の採用率計算が必要な理由と、このようなサンプルサイズが小さいデータの比率計算の問題について説明します。
その問題をふまえて、今回どのような推定を行いたいかを説明します。
弊社の成果報酬型求人サービスでは、応募だけでなく採用してもらうことで売上が発生します。そのため、応募率だけでなく採用率も重要になってきます。例えば、あまりに採用率が低い求人があれば、その求人にマッチした求職者に応募してもらうような施策を考えたり、採用方針を企業に問い合わせたりする必要があります。また、採用率が高い求人があれば、その理由を調べて他の求人の採用率を上げる施策に活かすこともできます。
採用率は採用数を応募数で割ることで計算しますが、バイト求人にしても転職求人にしても、求人ごとに集計すると安定した比率を得るだけの十分な応募数がある求人は少ないです。集計期間を長くとれば計算に使える応募数が多くなることもありますが、求人は入れ替わることも多いし、集計期間を長くすればするほど古い情報を反映した採用率になってしまうので好ましくありません。また、応募数が少なかった求人についても状況に応じて適切な対策を打ちたいので、応募数が少ない求人を無視するということもしたくありません。
当然ながら、採用率を計算するときの分母にあたる応募数が少ないと、算出された採用率の信頼性は低くなります。例えば、応募数200件で採用数100件の求人であれば採用率50%と言われてもあまり違和感がないですが、応募数2件で採用数1件だと採用率50%と言われても疑わしいですよね。特に応募数が少ないときに、極端な採用率が算出されてしまいやすいという問題があります。
それでは、全求人の平均採用率が20%であることがわかっていたらどうでしょう。多くの人は、各求人の応募数や採用数だけでなく全体的な傾向も考慮して、応募数が増えたときの採用率を推測するのではないでしょうか。例えば、応募数2件で採用数1件の求人の採用率は、応募数が増えていけば50%より低くなりそうですが、全体採用率20%よりは高そうなので、だいたい30〜40%ぐらいかなと考えませんか。一方、応募数200件で採用数100件の求人場合だと、分母の値も比較的大きいので採用率は50%より少し低めの45〜49%ぐらいかなと考えませんか。
このように全体的な傾向も考慮して採用率を計算できると便利です。今回はベイズ推定を使って、このような計算を行います。
主観的な事前分布を設定したベイズ推定
それでは、全求人の採用率傾向を考慮した各求人の採用率推定の考え方について説明します。
ベイズ推定では主観的な情報を事前分布として設定することができます。そのため、全求人の採用率の傾向を事前分布として設定すれば、全体傾向を考慮して各求人の採用率を推定することができそうです。
ベイズ推定では、データが少ないと事前分布の影響を強く受けますが、データが多くなってくると徐々に事前分布の影響が薄れてきます。そのため、応募数が少ないと、推定採用率はデータから単純に計算された採用率よりも全求人の採用率に近い値になります。一方で、応募数が多くなると、全求人の採用率よりデータから計算された採用率に近い値になります。その結果、前節で例として説明したような、人が直感的に判断したときと同じような推定採用率が得られることが期待できます。
事前分布の検討
今回の肝となる事前分布をどうするかについて説明します。
どのような事前分布を設定するのがよいかについては様々な考え方があるのですが、ここでは全求人の採用率傾向を表すことができ、計算が収束する分布を選ぶことにします。全求人の採用率傾向についてはデータを調べて検討することにしましょう。
ここからはサンプルデータを使って具体的に見ていきます。
サンプルデータ(クリックすると展開されます)
このサンプルデータは、ある条件で抽出した求人の応募数と採用数を模擬したデータになっています。1行が1求人に対応し、N、R、G列は推定に使うデータ、idとrateは参考のために付与したデータになっています。Nは応募数、Rは採用数、Gは地域や職種など何らかのグループを表すものと考えてください。rateは採用率で、idは説明の際に参照しやすいようにつけました。全体の採用数を応募数で割り、全体採用率を計算するとおよそ0.1766になります。全391求人のうち、応募が10件以上ある求人でも53しかなく、ほとんどの求人では採用率を計算しにくいことがわかると思います。
全体傾向を事前分布にするためには、採用率がどのような確率分布になるかを考える必要があります。まずは各求人の採用率をヒストグラムにして分布を見てみましょう。
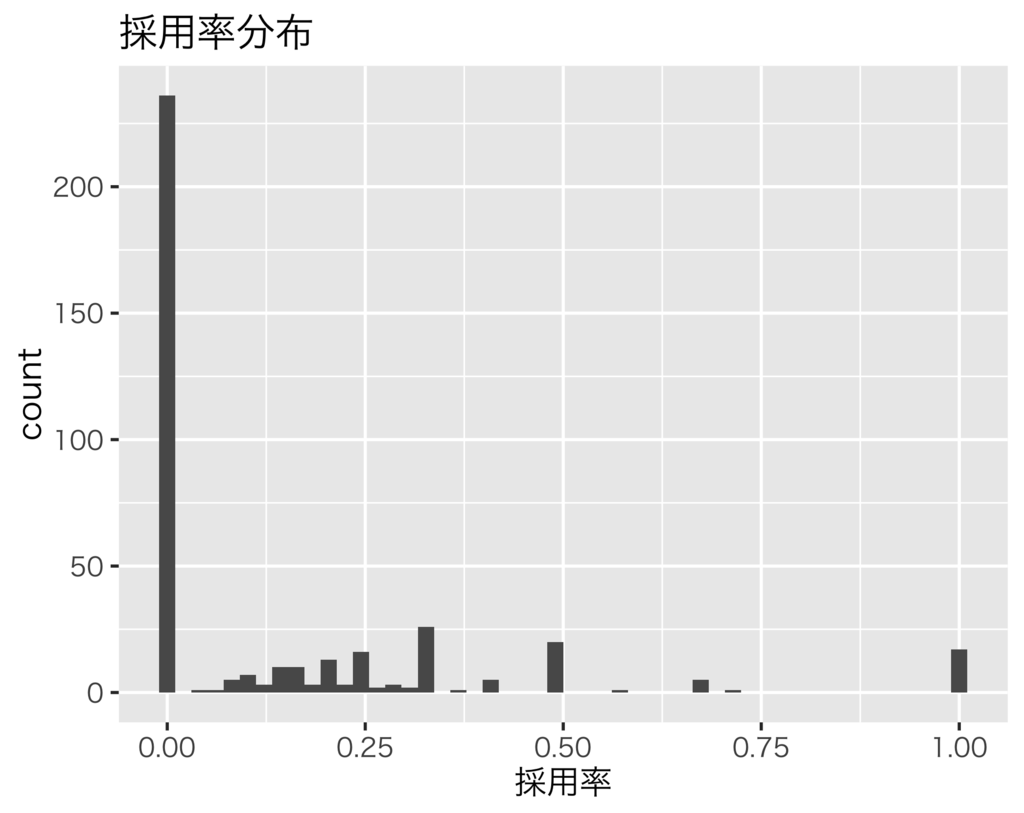
採用率0%が飛び抜けて多く、その他33%、50%、100%が多いことがわかりますが、これだけだと応募数が増えたときにどのような確率分布になるかわからないですね。知りたいのは応募数が多くなったときの採用率の分布なので、応募数が一定数以上の求人の採用率分布を見てみましょう。
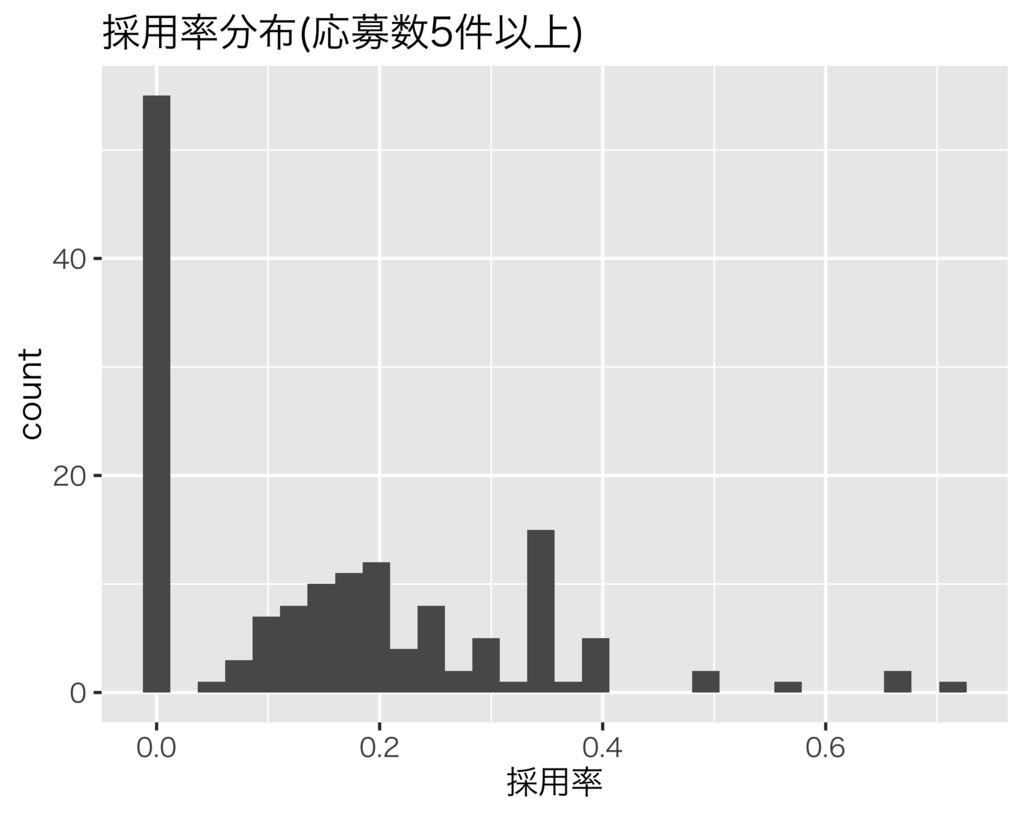
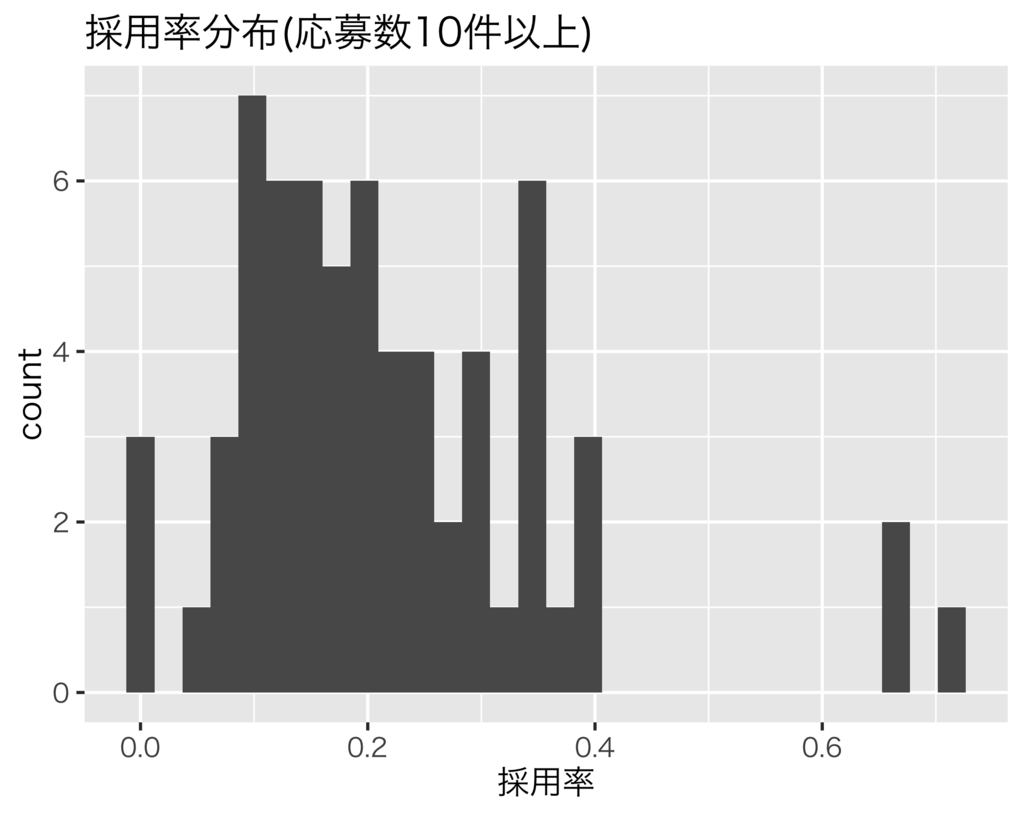
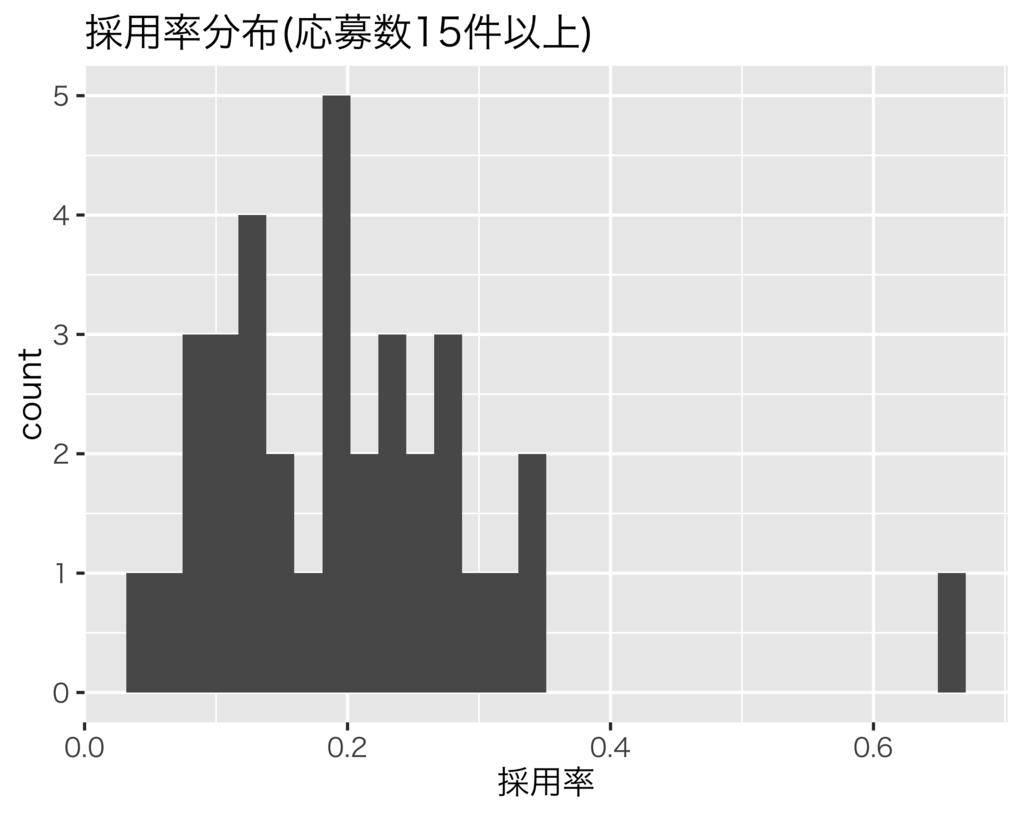
応募数が多い求人だけを見てみると、右裾の長い分布になっているように思えます。加えて、採用率0%や100%の求人もなくなっていることから、応募数が十分多いと採用率0%や100%の求人は0件になるのではと予想されます。そこで、このような特徴をもつ確率分布を探すとベータ分布が見つかります。これ以降はベータ分布を事前分布として使うことにしましょう。なお、採用率推定の事前分布としてベータ分布が常によいわけではありません。例えば、応募数が多いのに採用率100%の求人が多い場合はガンマ分布など別の分布を使うこともあります。
事前分布を活用した比率の推定
事前分布に使う確率分布も決めたので、実際に採用率を推定します。ここでは、前節で検討した事前分布の有無による違いを見るため、事前分布を使わないときと、事前分布に固定パラメータのベータ分布を使ったときの2種類の結果を調べます。
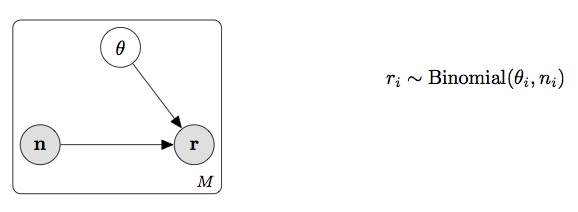
まず、採用率は二項分布にしたがうことだけを仮定したシンプルなモデルで推定してみましょう。Stanでは明示的に事前分布を指定しないと一様分布を指定したときと同じになります。モデルとコードは以下のようになります。
Rコード(クリックすると展開されます)
library(rstan) library(tidyverse) dat <- read_csv("sample.csv") stan_dat <- list(M = nrow(dat), N = dat$N, R = dat$R) fit <- stan(file = 'binom.stan', data = stan_dat, seed = 123)
Stanコード(binom.stan)(クリックすると展開されます)
data {
int M;
int<lower=0> N[M]; // 応募数(分母)
int<lower=0> R[M]; // 採用数(分子)
}
parameters {
vector<lower=0, upper=1>[M] theta; // 採用率
}
model {
R ~ binomial(N, theta);
}
推定結果のサマリは以下のようになります。
推定結果のサマリ(クリックすると展開されます)
単純に計算したときのように0%や100%のような推定採用率にはならないことがわかります。一方で、採用率の全体傾向がまったく考慮されていないため、応募1件採用0件の求人の採用率期待値がおよそ33%になるなど、採用率としては好ましくない結果も見られます。
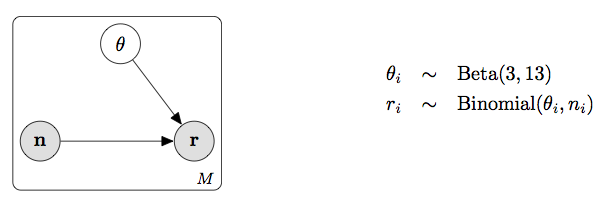
では、採用率の事前分布としてベータ分布を設定したモデルで推定してみましょう。ここではベータ分布のパラメータに\(\alpha=3\)と\(\beta=13\)を使います(理由は後述します)。固定パラメータを使うのでプレート図は同じで、モデルとコードは以下のように事前分布の部分が追加されます。
Rコード(クリックすると展開されます)
library(rstan) library(tidyverse) dat <- read_csv("sample.csv") stan_dat <- list(M = nrow(dat), N = dat$N, R = dat$R) fit <- stan(file = 'binom_beta.stan', data = stan_dat, seed = 123)
Stanコード(binom_beta.stan)(クリックすると展開されます)
data {
int M;
int<lower=0> R[M]; // 応募数(分母)
int<lower=0> N[M]; // 採用数(分子)
}
parameters {
vector<lower=0, upper=1>[M] theta; // 採用率
}
model {
R ~ binomial(N, theta);
theta ~ beta(3, 13); // 事前分布
}
推定結果のサマリは以下のようになります。
推定結果のサマリ(クリックすると展開されます)
まず、採用がないケースについて見てみると、応募1件採用0件の求人は採用率期待値がおよそ0.176、応募2件採用0件の求人は採用率期待値がおよそ0.166となっています。応募数が1〜2件程度と少なく不確実性が高いので、全体採用率0.1766よりやや低い値として算出されています。また、応募1件採用0件より応募2件採用0件のほうが採用率はより低い可能性が高いため、採用率も低めになっていることが確認できます。さらに、id=234の求人のように応募10件採用0件になると、採用率が低い可能性がさらに高まるので、採用率期待値はおよそ0.116と推定されています。逆に採用が多いケースについて見てみると、応募1件採用1件の求人の採用率期待値はおよそ0.235、応募3件採用3件の求人ではおよそ0.314と推定されています。データが少なく不確実性が高いことを考えると、これらの推定結果は直感的によさそうに思えます。
応募が多いほど推定もより正確になるので採用率の分布の幅はより狭くなります。例として、単純に計算した時の採用率が等しいid=302とid=308の二つの求人について見てみましょう。id=302は応募4件採用1件、id=308は応募72件採用18件の求人です。推定された各々の求人の採用率の分布は以下のようになります。
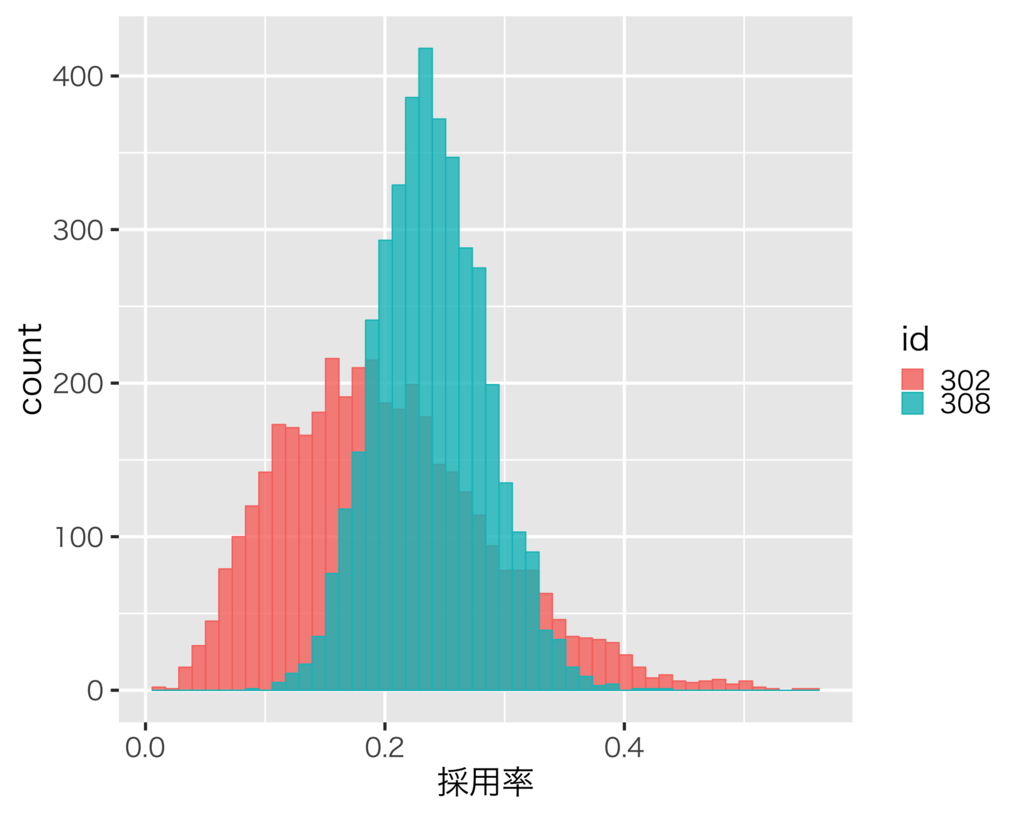
id=302は応募数が少ないので事前分布の影響を強く受けており、さらに不確実性も高いので分布の幅がid=308と比較して広いことがわかります。一方で、id=308は応募が比較的多いため事前分布の影響が弱く、さらに不確実性も低いので分布の幅が狭いことがわかります。
目論見どおりベータ分布を事前分布として設定することで、直感的によさそうな採用率が推定されているように見えます。しかし実は、推定結果がベータ分布のパラメータ\(\alpha\)、\(\beta\)の値に強く依存するという問題があります。そのため、ベータ分布のパラメータ\(\alpha\)、\(\beta\)を別の固定値に設定すると、全く異なる推定採用率になってしまいます。採用率のヒストグラムを見ても、応募の多い求人が十分にないため適切なパラメータ値まではよくわかりません。そこで、階層ベイズを使うことでベータ分布のパラメータも推定するようにします。
階層ベイズによる比率の推定
事前分布をうまく設定することができれば、直感的によさそうな採用率を推定できることがわかりました。しかし、その事前分布のパラメータをどのように設定すればよいかわからないという問題があることもわかりました。ここではこの問題に対処するため、事前分布のパラメータにも事前分布を設定する、いわゆる階層ベイズを使うことで、採用率の事前分布のパラメータも推定します。
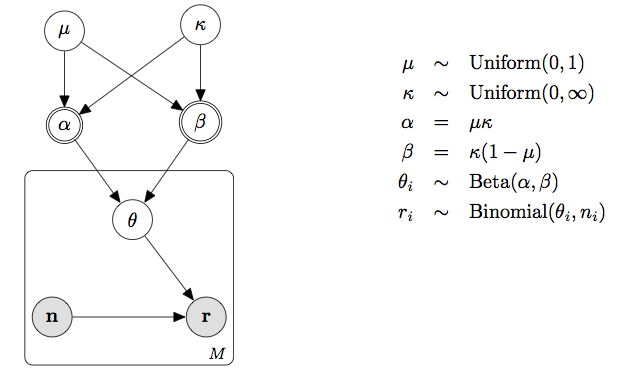
採用率の事前分布には今までと同じようにベータ分布を使いますが、ベータ分布のパラメータ\(\alpha\)、\(\beta\)にも事前分布を設定します。ここでは、後で扱いやすいように以下のような再パラメータ化を行います。\(\mu\)はベータ分布の期待値です。
\begin{eqnarray*}
\mu &=& \frac{\alpha}{\alpha + \beta} \\
\kappa &=& \alpha + \beta
\end{eqnarray*}
モデルとコードは以下のようになります。
Rコード(クリックすると展開されます)
library(rstan) library(tidyverse) dat <- read_csv("sample.csv") stan_dat <- list(M = nrow(dat), N = dat$N, R = dat$R) fit <- stan(file = 'hier.stan', data = stan_dat, seed = 123)
Stanコード(hier.stan)(クリックすると展開されます)
data {
int M;
int<lower=0> R[M]; // 応募数(分母)
int<lower=0> N[M]; // 採用数(分子)
}
parameters {
vector<lower=0, upper=1>[M] theta; // 採用率
real<lower=0, upper=1> mu; // 事前分布(ベータ分布)の期待値(= a / (a + b))
real<lower=0> kappa; // a + b
}
transformed parameters {
real<lower=0> a; // 事前分布(ベータ分布)のパラメータ
real<lower=0> b; // 事前分布(ベータ分布)のパラメータ
a = mu * kappa;
b = kappa * (1 - mu);
}
model {
R ~ binomial(N, theta);
theta ~ beta(a, b); // 事前分布
}
このようにすることで、モデルとデータに合った、事前分布のパラメータ(の分布)が推定されます。ベータ分布のパラメータに固定値のような強い制約を課すのではなく、分布のような緩やかな制約を使っているところがポイントです。採用率の事前分布の条件が緩和されたことで、データに応じてパラメータが自動的に推定されるようになります。階層ベイズの場合も事前分布の事前分布を変更すると推定結果は影響を受けるものの、パラメータがモデルとデータから大きく逸脱した値をとる確率は低くなるため、階層化せず事前分布のパラメータ固定値を変更した時ほど大きな影響は受けることは少ないです。そのため、このようなケースで階層ベイズを使うと恣意的に推定結果を操作するのが難しくなるので、結果の客観性が高まるというメリットもあります。
推定結果は以下のようになります。
推定結果のサマリ(クリックすると展開されます)
前節と同様に推定結果を確認すると、階層ベイズでも直感的によさそうな採用率が推定されているように見えますね。前節で使ったベータ分布の固定パラメータは、この階層ベイズのパラメータを参考にして決めました。なお、ハイパーパラメータの有効サンプルサイズが小さいところは気になるので、必要に応じてサンプリング数を増やすなどの対応が必要です。
グループの違いを考慮した階層ベイズによる比率の推定
採用率は職種や地域によって大きく異なることが知られています。そこで最後に、職種や地域のようなグループごとの採用率の違いも考慮した推定をやってみましょう。
基本的には今までやってきたことと同じように、採用率の事前分布の事前分布のパラメータにさらに事前分布を設定します。グループごとに採用率を推定することもできますが、職種や地域によっては応募が少ないため全体傾向すら推定できないグループがあることが多いです。そこで、求人の採用率の事前分布にグループごとの採用率を使い、グループごとの採用率(の期待値)の事前分布にグループ別採用率の分布を設定します。このように階層を増やすことで、応募が少ないグループの採用率の推定にはグループ別採用率の分布が利用されるため、推定がしやすくなります。なお、ここではデータの分布の傾向については確認しませんが、グループごとの採用率分布も、応募の多いグループ内の求人の採用率分布も、前節までに見てきた全求人の採用率分布とほぼ同じような傾向になっているので、引き続き事前分布にはベータ分布を使います。
モデルとコードは以下のようになります。モデルが複雑になり計算が不安定になりやすいので、ハイパーパラメータ\(\kappa_g\)と\(\kappa_i\)に半正規分布を設定して安定化を図っています。また、Stan実行時にオプションadapt_deltaを0.99に設定しています。
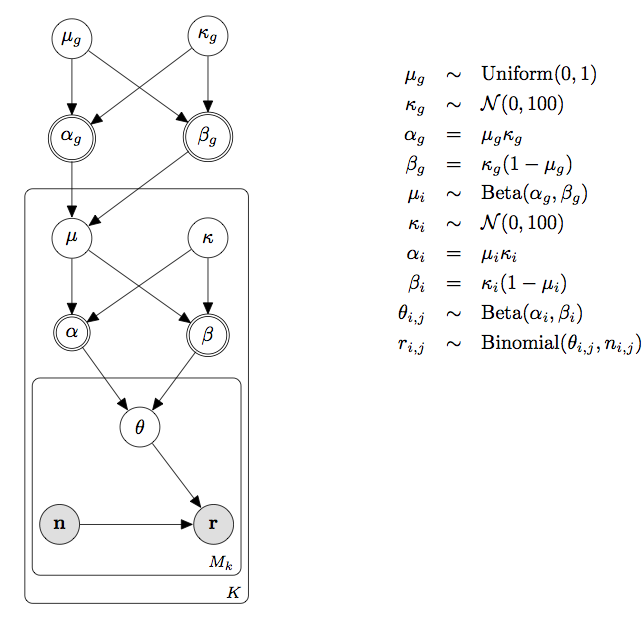
Rコード(クリックすると展開されます)
library(rstan) library(tidyverse) dat <- read_csv("sample.csv") stan_dat <- list(M = nrow(dat), K = dat$G %>% unique %>% length, N = dat$N, R = dat$R, G = dat$G) fit <- stan(file = 'hier2.stan', data = stan_dat, seed = 123, control = list(adapt_delta = 0.99))
Stanコード(hier2.stan)(クリックすると展開されます)
data {
int M; // データ数
int K; // グループIDの最大値
int<lower=0> N[M]; // 応募数(分母)
int<lower=0> R[M]; // 採用数(分子)
int<lower=1, upper=K> G[M]; // グループID
}
parameters {
real<lower=0, upper=1> theta[M]; // 採用率
vector<lower=0, upper=1>[K] mu; // グループ別の採用率事前分布のパラメータ(期待値)
vector<lower=0>[K] kappa; // グループ別の採用率事前分布ののパラメータ(alpha + beta)
real<lower=0, upper=1> mu_g; // グループの事前分布のパラメータ(期待値)
real<lower=0> kappa_g; // グループの事前分布のパラメータ(alpha + beta)
}
transformed parameters {
vector<lower=0>[K] a; // グループ別の事前分布(ベータ分布)のパラメータ
vector<lower=0>[K] b; // グループ別の事前分布(ベータ分布)のパラメータ
real<lower=0> a_g; // グループの事前分布(ベータ分布)のパラメータ
real<lower=0> b_g; // グループの事前分布(ベータ分布)のパラメータ
a = mu .* kappa;
b = kappa .* (1 - mu);
a_g = mu_g .* kappa_g;
b_g = kappa_g .* (1 - mu_g);
}
model {
R ~ binomial(N, theta);
for (i in 1:M) {
theta[i] ~ beta(a[G[i]], b[G[i]]); // 採用率の事前分布(パラメータはグループ別)
}
mu ~ beta(a_g, b_g); // グループの事前分布(採用率の事前分布のパラメータの事前分布)
kappa ~ normal(0, 100);
kappa_g ~ normal(0, 100);
}
結果は以下のようになります。
推定結果のサマリ(クリックすると展開されます)
応募数と採用数が同じでも、グループによって推定採用率に違いがあることが確認できます。例として、推定採用率が比較的高いG=18に所属しているid=41の求人と、推定採用率が比較的低いG=24に所属しているid=35の求人について見てみましょう。どちらも応募1件採用0件ですが、推定採用率の期待値はそれぞれ0.215、0.1と異なっており、id=41のほうが高いことがわかります。期待通り、グループの違いが推定採用率に反映されていることがうかがえます。
一方で、データがほとんど変わらないのにパラメータが増えモデルが複雑になっているため、収束しにくくなっていることもわかると思います。ハイパーパラメータ\(\kappa_i\)の事前分布への依存性も高く、頑健性は高くありません。実務で利用する場合は、グループごとの違いが反映されるメリットと、計算が不安定化するデメリットを比較してどのモデルを使うかを決めることになると思います。また、より客観的にモデル選択をしたいのであれば、WBICを使う方法もあります。
最後に注意点を述べておこうと思います。今回のような推定結果を利用するときに気をつけなければいけいないことは、結果が事前分布や全体傾向に依存しているところです。事前分布を変更すると異なる推定値が得られることはよくありますし、データの抽出条件によって全体傾向が違うため抽出条件ごとに異なるモデルが必要とされることもあります。また、商品設計が変更されたり時間が経過したりしてデータの全体傾向が変わると、個別のデータの特徴には変化がなくとも事前分布が全体傾向に適合しなくなる可能性があるので注意が必要です。例えば、求人メディアの場合では、異なる採用率傾向をもつ求人が増えると全体傾向が変わる可能性があるので、事前分布の再検討が必要になるかもしれません。
まとめ
今回は階層ベイズを使って採用率などの分母が小さい比率を推定する方法を紹介しました。ポイントは以下の二点です
- 個別に見るとデータ量が少なくてまともな推定が難しそうでも、全体傾向などをうまく利用すると推定が可能になることがある
- 階層ベイズを利用することで事前分布のパラメータ(の分布)を自動的に推定できることがある
似たような方法は比率だけでなく別の小標本データにも応用できます。弊社にはベイズ統計に理解のあるディレクターもいるため、今回のようなベイズ推定結果を活用した取り組みも行われています。
なお、元ネタは統計モデリングの社内勉強会で階層ベイズを説明するときに使ったものです。この勉強会に参加したアナリストにもエンジニアにも受けがよかったのでブログ記事にしてみました。今後は小ネタでも役立ちそうなものがあれば紹介していこうと思います。
