こんにちは、リブセンスでデータサイエンティストをしている北原です。今回は平均処置効果の推定方法について紹介します。より具体的にはマッチングや重み付けといった共変量のバランシングを利用してバイアスの小さい推定をする方法を使い、複数得られた推定結果を絞り込んで意思決定に使える結論を得るまでの流れを扱います。サンプルデータを使って実際に推定を行い結果を解釈するところまで行います。コードはRです。完全にコンセンサスのとれた因果推論方法・手順はおそらく存在しないので、現時点でよいのではと考えている方法の紹介になります。
今回紹介する方法のポイントは、共変量のバランシングによってモデル依存性が低下することを利用して信頼できそうな推定結果を絞り込んでいるところにあります。手法やモデルによって様々な推定値が得られますが、バイアスの評価方法がないため採用すべきものがわからないという問題があります。しかし、共変量のバランスがとれることでモデル依存性が低下すると推定値が安定するため、妥当な推定値をある程度絞り込むことができます。これにより全く見当違いな結果を採用することを回避できるのではと考えています。実際には共変量のバランス以外にも考慮すべき事項があるので、本記事ではそれらについても合わせて紹介します。なお、この方法は推定結果を見てから意思決定をしているので、不適切とされることも多いのでご注意ください。
リブセンスで観察データを使った因果推論が必要とされるのは、A/Bテストが困難な施策の効果検証を行いたいときが多いです。そこで今回はA/Bテストと同じくAverage Treatment Effect(ATE、平均処置効果)をmarginal effectとして推定するケースのみを扱います。また、処置は2値で結果は連続値のときのみを扱います。WebサービスのA/Bテストは医療や政策の効果検証ほどシビアなことは少ないので、施策の採否判断に使える程度の結果が得られればOKと考えて使っています。
Webサービスでの因果推論
施策の正確な効果推定を行いたいならば可能な限りA/Bテスト、因果推論分野でいうRandomized Controlled Trial(RCT、ランダム化比較試験)、を実施したほうがよいです。観察データを使った因果推論よりはA/Bテストのほうがはるかに簡単かつ精度も高いです。
しかし、ときには観察データを使った因果推論が必要なこともあります。A/Bテストで得られるものと同じ結果を得られることはあまりないのですが、サービスの性質やユーザーの公平性の問題がありA/Bテストがやりにくいときや、A/Bテストなしで実施済みの施策の効果検証をしたいときには必要になります。例えば、転職ドラフトの年収非公開施策では、サービスの性質やユーザーの公平性の問題がありA/Bテストを実施しませんでした。
医療や政策の因果推論では高い信頼性がもとめられますが、WebサービスのA/Bテストの代わりに使う程度であればそこまで高い精度がもとめられることは少ないでしょう。施策を継続するかどうかという判断ができればよいです。そのため、最低限抑えるべきことは抑えつつ、なるべく手軽に使えるようにしたいというのが基本スタンスです。そこで、現在は次のような方針をとっています。
共変量選択には、VanderWeeleの共変量選択の原則(VanderWeele, 2019)を使います。Directed Acyclic Graph(DAG)を書いてバックドア基準をチェックすべきですが、これは大変です。DAGが書けるほどA/Bテスト対象について深く理解できていることは少ないですし、理解していたとしてもDAGを書くのは簡単ではありません。最適な共変量ではなくとも致命的なバイアスの混入を避けられればよいという考えです。(VanderWeele, 2019)で紹介されている方法は、DAGを書かなくとも適切な共変量を選択し不適切な共変量選択によるバイアスを回避できるようになっています。
基本的には、共変量のバランスを基準に採用する結果を決めます。観察データの因果推論では手法やモデルによって異なる推定値が得られることが多く、どの結果を最終的に採用するかを決める必要があります。共変量のバランスがとれればバイアスが減りモデル依存性や未観測の欠落変数の影響も小さくなると考えられるので、基本的には共変量のバランスがよいものを採用します。この考え方は(Ho et al., 2007)以降多くの研究で検証されてきていますし、マッチングだけでなく重み付けでも推奨されており(Austin & Stuart, 2015)、最近ではほぼコンセンサスがとれているのではないかと思います。ただし、共変量のバランスがよくとも、マッチングされないデータが多すぎたり、異なるサンプル同士がマッチングされていたり、重みが異常に大きかったりする場合など何らかの問題があるときは採用しません。また、共変量のバランスがとれていても推定値が大きくばらつく場合は、観測済み共変量とは独立もしくは相関が低くかつ結果への影響が大きい未観測共変量が存在する可能性が高く、本記事で扱っているような共変量のバランシングに基づく効果推定は断念します。
共変量のバランシングには複数の手法・モデルを使います。どのような手法・モデルを使えば共変量のバランスよくなるかは事前にはわからないためです。実際にはバランシングがうまくいきやすい手法やモデルがないわけではないのですが、あらゆるデータでうまくいくわけではありません。また、複数の手法・モデルを試みることでバランシングしにくい共変量や推定値の水準を知ることができるので結果の判断に役立ちます。複数の手法・モデルを扱うのは大変ですが、cobalt、WegihtIt、MatchItといったパッケージを利用することで効率化を図ることができます。なお、手法やモデルの選択については有名なガイダンス(Stuart, 2010)と、パッケージのvignettes(cobalt、 Matchit、Weightit)を参考にしています。
効果の推定値だけでなく標準誤差や信頼区間も算出します。データの不確実性を考慮すると標準誤差や信頼区間を確認するのは当然ではあるのですが、それに加えて推定値だけでは結果の判断がしにくいという実用上の問題もあります。手法やモデルによって異なる推定値が得られることが多いので、標準誤差や信頼区間まで確認しないと誤差と対処すべき分析上の問題とを判別するのが難しいです。標準誤差や信頼区間の計算方法についてはコンセンサスのとれたものがないと思いますが、基本的にはMatchItのvignettesに記載されている方法を使います。誤差の均一性や独立性は仮定しません。また、マッチングや重み付けの後に共変量による再調整を行います。
共変量のバランシングではマッチングと重み付けの双方を試みます。マッチングと重み付けでは潜在的結果の扱いなど特徴が異なるため、念のため双方の推定結果を見て総合的な解釈をするようにしています。推定結果がほぼ同じであれば結果の信頼性が高まりますし、異なっている場合はその原因を考えることで効果の特徴がわかります。(King & Nielsen, 2019)の指摘に基づき、マッチングでは傾向スコア以外の結果を重視します。
適切な推定ができているかは共変量のバランスがよくなることでモデル依存性が低下しているかで判断します。共変量のバランスがとれればバイアスが減りモデル依存性や未観測の欠落変数の影響も小さくなるので推定値が安定するはずです。そこで、共変量のバランスがよくなるにつれてモデル依存性が低下しているかを確認し、モデル依存性が低下していると判断できる推定値を使って結果の解釈をします。複数の推定結果を見てから採用する結果を選択しているので、恣意的に都合のよい結果を選択することが可能なため不適切とされることも多いです。しかし、長年の蓄積がある疫学や経済学において専門家が因果推論を行うケースとは異なり、Webサービスでは今まで因果推論が試みられたことのないデータに対して非専門家が因果推論を行うことが多いので、共変量のバランス等の前処理段階の諸条件のみを基準に最終結果を得ようとすると誤った結果を選択してしまう可能性が高くなるのではという懸念があります。そこで、現実的な対処方法としてこのような方法をとっています。
ここからは実際にデータを使って共変量のバランシングと推定、結果の選定・解釈まで行っていきます。
本記事ではサンプルデータとして岩波データサイエンス Vol.3の加藤、星野による記事「因果効果推定の応用」で使われている疑似データを利用させていただきます。これはCM接触有無(cm_dummy)によるスマートフォンアプリ使用状況を表したデータです。今回は利用時間(gamesecond)の推定を行います。より具体的には、母集団全体におけるCM接触がアプリ利用時間に与える効果であるATE、marginal effectを推定します。データ項目の詳細などについてはサポートサイトの補論をご覧ください。本記事で必要なライブラリとデータの読み込みは以下のとおりです。
library(tidyverse) library(broom) library(furrr) library(cobalt) library(MatchIt) library(WeightIt) library(lmtest) library(sandwich) library(knitr) df_ds3 <- read_csv("https://raw.githubusercontent.com/iwanami-datascience/vol3/master/kato%26hoshino/q_data_x.csv")
共変量の選択
選択基準
共変量の選択では(VanderWeele 2019)で推奨されているmodified disjunctive cause criterionもしくはpre-treatment criterionを使います。ドメイン知識がある場合は前者、ない場合は後者を使います。DAGを書かずに使えるところがポイントです。この共変量選択方法については、こちらの記事(「回帰分析における「調整変数」の選び方:実践編」)が参考になると思います。
共変量の選択では、不適切な共変量を使うことによるバイアスの混入と、有効な共変量の欠落と不要な共変量の使用による効率の低下が問題になります。適切な推定を行うためにはバイアスの混入は回避しなければなりませんが、効率の低下はある程度許容できます。欠落変数のようによく知られているもの以外にも、因果構造に起因するバイアスの混入は、中間変数と合流バイアス、操作変数によって生じることが知られており、VanderWeeleの提案もこれらに配慮したものになっています。
ドメイン知識がある場合はmodified disjunctive cause criterionを使います。
- 処置あるいは結果、もしくは双方の原因になっている共変量を選択
- ただし、操作変数を除外する
- 処置と結果双方の原因になっている未観測共変量の代理変数を含める
上記の基準だけでは中間変数も選択されてしまうので、「処置より前に収集された共変量」を選択することが暗黙の前提になっていると思われます。
操作変数は処置の原因になっているが結果の直接的な原因にはなっていない変数です。操作変数は探しても見つからないぐらいレアなので、ほとんどのケースでは気にしなくとも問題ないと思います。もし処置の説明能力の高い操作変数が存在する場合、操作変数法の利用を検討すべきです。
また、ここでいう未観測共変量の代理変数というのは、未観測共変量から影響を受ける変数のことです。未観測共変量が処置あるいは結果のいずれかの原因でしかない場合は合流バイアスが生じる原因になるため、双方の原因であることが知られているときのみ代理変数を含めます。
ドメイン知識がない場合はpre-treatment criterionを使います。
- 処置、結果のいずれよりも前に収集されたデータの変数を選択
これは簡単に使えるものの、合流バイアスもしくはMバイアスと呼ばれるものが生じる可能性があります。ただし、合流バイアスは直接的間接的問わず処置と結果のいずれの原因でもない共変量を選択しているときにしか発生しません。そのため、処置や結果とまったく無関係な共変量を使っていない限りはあまり気にしなくてもよいかもしれません。
今回のサンプルデータの場合、計測条件が明らかではないので元記事の結果を再現するのに使われている共変量はCM接触前に計測されていると仮定します。これによりpre-treatment criterionを満たします。ドメイン知識がないのでmodified disjunctive cause criterionは使えません。TV視聴時間の計測がCM接触と同時もしくはそれ以降になされていることはありうるので、実務ではデータがどのように取得されたかを確認する必要があります。この仮定に基づき、以降はサポートサイトで公開されているコードと同じ共変量を使います。
cov_names <- c("TVwatch_day", "age", "sex", "marry_dummy", "child_dummy", "inc", "pmoney", "area_kanto", "area_tokai", "area_keihanshin", "job_dummy1", "job_dummy2", "job_dummy3", "job_dummy4", "job_dummy5", "job_dummy6", "job_dummy7", "fam_str_dummy1", "fam_str_dummy2", "fam_str_dummy3", "fam_str_dummy4")
共変量のバランス
cobaltパッケージのbal.tab()関数を使って共変量のバランスを確認してみましょう。cobaltは共変量のバランス評価を容易にさせるツールです。cobaltの使い方についてはvignettesをご参照ください。
ds3_formula <- f.build("cm_dummy", cov_names) # バランス確認 bal_tab_orig <- bal.tab( ds3_formula, data = df_ds3, s.d.denom = "pooled", disp = c("means", "sds"), stats = c("mean.diffs", "variance.ratios", "ks.statistics"), thresholds = c(m = 0.1, v = 2) ) bal_tab_orig
Balance Measures
Type M.0.Un SD.0.Un M.1.Un SD.1.Un Diff.Un M.Threshold.Un V.Ratio.Un V.Threshold.Un KS.Un
TVwatch_day Contin. 5714.9823 5690.3713 11461.8813 8851.0912 0.7724 Not Balanced, >0.1 2.4194 Not Balanced, >2 0.3301
age Contin. 40.1872 10.6365 41.7671 10.1484 0.1520 Not Balanced, >0.1 0.9103 Balanced, <2 0.0732
sex Binary 0.6711 . 0.5968 . -0.0743 Balanced, <0.1 . 0.0743
marry_dummy Binary 0.6305 . 0.6704 . 0.0399 Balanced, <0.1 . 0.0399
child_dummy Binary 0.4220 . 0.4245 . 0.0025 Balanced, <0.1 . 0.0025
inc Contin. 369.2459 264.4870 341.6972 270.6953 -0.1029 Not Balanced, >0.1 1.0475 Balanced, <2 0.0766
pmoney Contin. 3.5580 3.3603 3.5443 3.4028 -0.0041 Balanced, <0.1 1.0255 Balanced, <2 0.0306
area_kanto Binary 0.0630 . 0.1310 . 0.0680 Balanced, <0.1 . 0.0680
area_tokai Binary 0.1245 . 0.0931 . -0.0313 Balanced, <0.1 . 0.0313
area_keihanshin Binary 0.3034 . 0.0746 . -0.2289 Not Balanced, >0.1 . 0.2289
job_dummy1 Binary 0.6006 . 0.5176 . -0.0830 Balanced, <0.1 . 0.0830
job_dummy2 Binary 0.0570 . 0.0502 . -0.0068 Balanced, <0.1 . 0.0068
job_dummy3 Binary 0.0688 . 0.0859 . 0.0171 Balanced, <0.1 . 0.0171
job_dummy4 Binary 0.0114 . 0.0135 . 0.0021 Balanced, <0.1 . 0.0021
job_dummy5 Binary 0.0907 . 0.1559 . 0.0652 Balanced, <0.1 . 0.0652
job_dummy6 Binary 0.0920 . 0.1110 . 0.0190 Balanced, <0.1 . 0.0190
job_dummy7 Binary 0.0464 . 0.0306 . -0.0158 Balanced, <0.1 . 0.0158
fam_str_dummy1 Binary 0.1504 . 0.1445 . -0.0059 Balanced, <0.1 . 0.0059
fam_str_dummy2 Binary 0.1281 . 0.1684 . 0.0404 Balanced, <0.1 . 0.0404
fam_str_dummy3 Binary 0.6190 . 0.6223 . 0.0033 Balanced, <0.1 . 0.0033
fam_str_dummy4 Binary 0.0835 . 0.0507 . -0.0328 Balanced, <0.1 . 0.0328
Balance tally for mean differences
count
Balanced, <0.1 17
Not Balanced, >0.1 4
Variable with the greatest mean difference
Variable Diff.Un M.Threshold.Un
TVwatch_day 0.7724 Not Balanced, >0.1
Balance tally for variance ratios
count
Balanced, <2 3
Not Balanced, >2 1
Variable with the greatest variance ratio
Variable V.Ratio.Un V.Threshold.Un
TVwatch_day 2.4194 Not Balanced, >2
Sample sizes
Control Treated
All 5856 4144
共変量のバランスは主にStandardized Mean Difference(SMD)と分散比でチェックします。Balance MeasuresのDiff.UnがSMD、V.Ratio.Unが分散比です。なお、末尾についている".Un"は共変量バランシング前のデータであることを示しています。SMDは0に近いほどよく、分散比は1に近いほどよいです。SMDの計算方法については(Austin, 2009)などをご参照ください。SMDとバイアスとの相関が高いことは(Stuart, 2013)などいくつかの研究で示されています。共変量のバランスを表す指標は複数あるものの、SMDが最もよく使われているのではないかと思います。
Kolmogorov-Smirnov(KS)統計量もバランス指標の一つです。Balance MeasuresのKS.UnがKolmogorov-Smirnov(KS)統計量です。KS統計量は経験累積分布の差の最大値で確率分布が異なるかを検定するときに使われます。0から1までの値をとり分布が異なるほど1に近づきます。SMDではわからない分布の違いを調べるのに便利な指標です。KS統計量は利用を推奨している研究もあれば、SMDと比較して劣るという研究もあるのでバランシングでは参考程度に確認しておくぐらいでよいかもしれません。
バランスがとれていると判断できる明確な閾値があるわけではないのですが、SMDは0.1以下、分散比は0.5〜2に収まることを目安にしているケースが多いようです。SMDは小さいほどよく、MatchItのvignettesでは結果に大きく影響する共変量については0.05以下にすることが推奨されています。一つの指標が改善されて共変量のバランスがとれると他の指標も改善することが多いので、一番よく使われるSMDを基準にバランシングを行い同時に他の指標もチェックするという進め方が多いのではと思います。
このサンプルデータでは、SMDは4つがアンバランス、分散比は1つがアンバランスであることがわかります。特にTVwatch_dayのSMDが一番大きく0.7724となっています。次節以降ではこれらのアンバランスがなるべくなくなるよう調整していきます。この例では交互作用や高次のバランスのチェックはしていませんが、より信頼性の高い推定をする場合はこれらについてもチェックすることが推奨されています。
マッチング
マッチングはAverage Treatment effect on the Treated(ATT)向きの手法ですが、処置群と対照群ともに類似サンプルが十分存在するならばフルマッチングを使うことでATEを計算できます。今回使っているサンプルデータは処置群と対照群が同程度なので類似サンプルが十分存在すると仮定してマッチングでもATEを計算します。ただし、最も近いサンプル同士でも類似とは言い難いペアが存在することがあるのでcaliperも使います。
マッチングにはMatchItパッケージを使います。MatchItは(Ho et al., 2007)を実装したものですが、傾向スコアを算出するパッケージの共通インターフェースを提供するラッパーにもなっています。そのため、マッチングで複数の手法やモデルを使うときに適しています。
最初にMatchItの使い方や推定方法を説明し、その後に推定結果を得る一連の流れを説明します。
MatchItの使い方
まずMatchItの使い方を説明します。詳細はvignettesをご参照ください。ここではマハラノビス距離を使ったマッチングを例にします。
マッチング
以下を実行するとマハラノビス距離を使ったフルマッチングができます。
m.out <- matchit( ds3_formula, data = df_ds3, estimand = "ATE", method = "full", distance = "mahalanobis") summary(m.out, un = FALSE)
Call:
matchit(formula = ds3_formula, data = df_ds3, method = "full",
distance = "mahalanobis", estimand = "ATE")
Summary of Balance for Matched Data:
Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean eCDF Max Std. Pair Dist.
TVwatch_day 10519.3416 6113.9285 0.5921 1.9087 0.1800 0.2872 0.7360
age 41.4109 40.4809 0.0895 0.9003 0.0199 0.0562 0.4148
sex 0.6425 0.6403 0.0047 . 0.0022 0.0022 0.1605
marry_dummy 0.6503 0.6467 0.0076 . 0.0036 0.0036 0.0713
child_dummy 0.4280 0.4248 0.0064 . 0.0032 0.0032 0.1328
inc 355.5755 357.5834 -0.0075 1.0579 0.0142 0.0259 0.2863
pmoney 3.4375 3.5801 -0.0422 0.8717 0.0130 0.0340 0.4292
area_kanto 0.1069 0.0755 0.1068 . 0.0314 0.0314 0.0898
area_tokai 0.0946 0.1244 -0.0960 . 0.0298 0.0298 0.1302
area_keihanshin 0.1315 0.2738 -0.3802 . 0.1423 0.1423 0.3929
job_dummy1 0.5589 0.5735 -0.0295 . 0.0146 0.0146 0.0434
job_dummy2 0.0513 0.0571 -0.0258 . 0.0058 0.0058 0.0211
job_dummy3 0.0767 0.0751 0.0060 . 0.0016 0.0016 0.0135
job_dummy4 0.0123 0.0123 -0.0000 . 0.0000 0.0000 0.0000
job_dummy5 0.1258 0.1096 0.0495 . 0.0162 0.0162 0.0466
job_dummy6 0.1012 0.0986 0.0086 . 0.0026 0.0026 0.0158
job_dummy7 0.0399 0.0399 -0.0000 . 0.0000 0.0000 0.0000
fam_str_dummy1 0.1512 0.1448 0.0180 . 0.0064 0.0064 0.0296
fam_str_dummy2 0.1507 0.1387 0.0338 . 0.0120 0.0120 0.0439
fam_str_dummy3 0.6229 0.6181 0.0099 . 0.0048 0.0048 0.0835
fam_str_dummy4 0.0583 0.0815 -0.0929 . 0.0232 0.0232 0.0880
Sample Sizes:
Control Treated
All 5856. 4144.
Matched (ESS) 3878.32 1533.61
Matched 5856. 4144.
Unmatched 0. 0.
Discarded 0. 0.
今回はATEを推定するのでestimandには"ATE"を指定し、フルマッチングを使うのでmethodには"full"を指定します。ATEには対応していないmethodを使うとエラーになります。distanceでは距離や傾向スコアを計算する手法を指定します。例えば、ロジスティック回帰を使った傾向スコアマッチングを行う場合はdistanceに"glm"を指定します。マハラノビス距離以外は傾向スコアを使ったマッチングになっています。
summary()関数を使うとSMDと分散比、経験累積分布がマッチング前と後、改善率について表示されます。Summary of Balance for Matched DataのStd. Mean Diff.がSMD、Var. Ratioが分散比、eCDF Maxが経験累積分布の最大値です。なお、経験累積分布の最大値はKS統計量と同じです。マッチング後のサマリにはStd. Pair Dist.にペア同士の差が表示されています。類似サンプル同士をマッチングできていないとこの値が大きくなります。
全体傾向を視覚的に確認する場合はcobaltパッケージのlove.plot()関数が便利です。love.plot()の詳細についてはvignettesをご参照ください。
love.plot( m.out, stats = c("m", "v", "ks"), abs = TRUE, thresholds = c(m = .1, v = 2), var.order = "unadjusted", binary = "std", position = "bottom" )

TVwatch_dayとarea_keihanshinのSMDがマッチング後も基準となる0.1を大きく上回っていることが視覚的に確認できます。
バランスを分布で確認する場合はcobaltパッケージのbal.plot()関数が便利です。以下はバランスが一番悪いTVwatch_dayの分布です。
bal.plot(m.out, var.name = "TVwatch_day", which = "both", type = "histogram", mirror = TRUE)
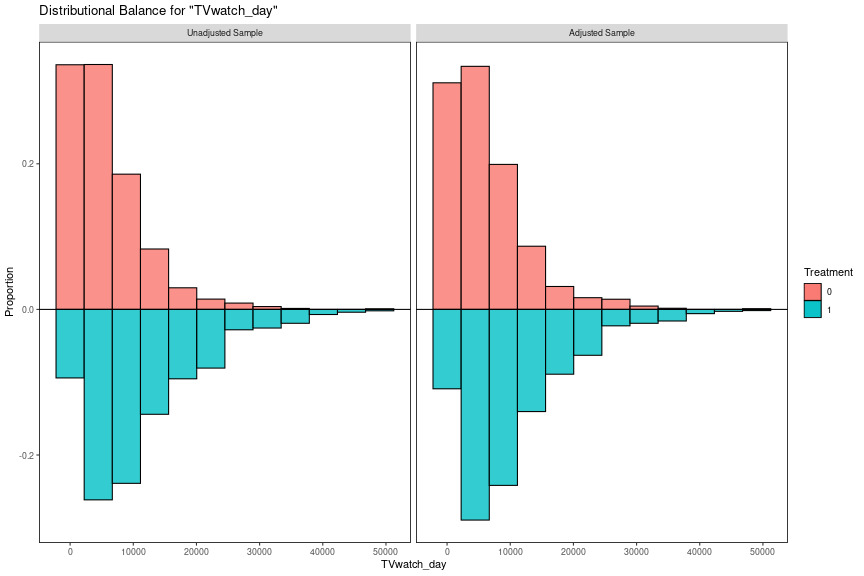
マッチング後もcm_dummyが0だとTVwatch_dayが小さいほうに偏っていることがわかります。またマッチング前を見るとTVwatch_dayが一定以上だとcm_dummyはほとんどが1であることもわかります。無理にマッチングさせるとTVwatch_dayが大きく異なるサンプル同士をペアにしなければならなくなることが予想されます。
マッチングでは共変量のバランスだけでなく、どれだけ類似サンプル同士をマッチングさせられるかも重要です。フルマッチングではcaliperなしだと全てのサンプルについてペアが作成されますが、caliperを使うとマッチできないサンプルが生じます。caliperは共変量ごとに名前付きベクトルで指定します。傾向スコアにcaliperを設定することが多いですがここではマハラノビス距離を使っているので、4つの共変量に0.1を設定しています。デフォルトでは標準化した値にcaliperが設定されますが、生の値にcaliperを設定することもできます。
calipers <- rep(0.2, 4) names(calipers) <- c("TVwatch_day", "age", "inc", "pmoney") m.out_c <- matchit( ds3_formula, data = df_ds3, estimand = "ATE", method = "full", distance = "mahalanobis", caliper = calipers) summary(m.out_c, un = FALSE) love.plot(m.out_c, stats = c("m", "v", "ks"), abs = TRUE, thresholds = c(m = .1, v = 2), var.order = "unadjusted", binary = "std", position = "bottom")
Call:
matchit(formula = ds3_formula, data = df_ds3, method = "full",
distance = "mahalanobis", estimand = "ATE", caliper = calipers)
Summary of Balance for Matched Data:
Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean eCDF Max Std. Pair Dist.
TVwatch_day 5693.7109 5503.8410 0.0255 0.9770 0.0165 0.0666 0.1024
age 39.2850 39.2850 0.0000 1.0010 0.0000 0.0000 0.0000
sex 0.5918 0.6329 -0.0857 . 0.0412 0.0412 0.6465
marry_dummy 0.6628 0.6344 0.0596 . 0.0284 0.0284 0.5871
child_dummy 0.4662 0.4473 0.0384 . 0.0190 0.0190 0.7428
inc 327.1241 327.0206 0.0004 0.9931 0.0018 0.0102 0.0225
pmoney 2.7100 2.7100 0.0000 1.0010 0.0000 0.0000 0.0000
area_kanto 0.1332 0.0620 0.2422 . 0.0712 0.0712 0.5379
area_tokai 0.0874 0.1285 -0.1323 . 0.0411 0.0411 0.5757
area_keihanshin 0.0666 0.2770 -0.5619 . 0.2104 0.2104 0.7479
job_dummy1 0.5306 0.5210 0.0194 . 0.0096 0.0096 0.3702
job_dummy2 0.0510 0.0593 -0.0366 . 0.0082 0.0082 0.4606
job_dummy3 0.0825 0.0851 -0.0096 . 0.0026 0.0026 0.4987
job_dummy4 0.0136 0.0107 0.0265 . 0.0029 0.0029 0.2066
job_dummy5 0.1323 0.1280 0.0131 . 0.0043 0.0043 0.3527
job_dummy6 0.1092 0.0927 0.0547 . 0.0165 0.0165 0.1701
job_dummy7 0.0491 0.0673 -0.0949 . 0.0183 0.0183 0.1566
fam_str_dummy1 0.1455 0.1477 -0.0062 . 0.0022 0.0022 0.6208
fam_str_dummy2 0.1524 0.1299 0.0635 . 0.0225 0.0225 0.6465
fam_str_dummy3 0.6189 0.6131 0.0120 . 0.0058 0.0058 0.8685
fam_str_dummy4 0.0710 0.0934 -0.0895 . 0.0223 0.0223 0.5842
Sample Sizes:
Control Treated
All 5856. 4144.
Matched (ESS) 1824.13 663.71
Matched 2639. 1915.
Unmatched 3217. 2229.
Discarded 0. 0.

この例ではcaliperを設定したTVwatch_dayなどのバランスは改善されていますが、他のarea_keihanshinなどがあまり改善されていないことがわかります。また、Sample SizesのUnmatchedを確認すると、半数程度のサンプルがマッチングできていないことがわかります。caliperを小さく設定するとcaliperを設定した共変量についてはペア同士の差が小さくなりますが、マッチできないサンプルが増えます。マッチできないサンプルが増えすぎると本来推定したいATEとは乖離したものを推定することになるので注意が必要です。caliperの適正値はケースバイケースなので、複数の値について調べる必要があります。
推定
推定値は回帰を利用して調べます。標準誤差の推定方法についてはコンセンサスのとれた方法はないようですが、本記事ではMatchItのvignettesに記載されている方法を使います。その場合、マッチング手法や結果変数の種類によって推定方法が異なります。本記事ではフルマッチングかつ結果変数が連続値の場合のみを扱います。それ以外のケースについてはMatchItのvignettesをご参照ください。
MatchItのvignettesでは推定値を計算する結果の回帰モデルに共変量を含めることバランスの再調整をすることを推奨しています。共変量を含めることで精度向上やマッチング後も残っているアンバランスの調整、doubly robustな効果が期待できるためです。結果の回帰モデルが誤っていた場合のバイアス混入の懸念がありますが、マッチング後も残っているアンバランスの影響を知るためにも、本記事では共変量を含める場合と含めない場合の2種類を試みます。マッチングによるバランシングがうまくいっていれば、再調整をしても推定値は再調整なしのときと大きく変わらないはずなので、アンバランスの影響が残っているかを確認することができます。
共変量を含めるかに関わらず推定にはマッチしたデータのみを使います。以下でマッチしたデータのみを抽出できます。
md <- match.data(m.out) head(md %>% dplyr::select(cm_dummy, weights, subclass))
# A tibble: 6 x 3
cm_dummy weights subclass
<dbl> <dbl> <fct>
1 0 0.590 586
2 0 1.17 1680
3 0 0.651 3055
4 0 0.612 2564
5 0 0.781 3271
6 0 1.17 240
weightsは処置の種類や処置の有無、マッチした数に応じて計算される重みです。多くのサンプルとマッチすると重みが大きくなります。subclassはマッチしたペアのグループです。
結果変数の回帰モデルに共変量を含めない場合は次のように推定します。ここでは推定値とその誤差、信頼区間の計算にはlmtestパッケージのcoeftest()関数とcoefci()関数を使います。また、クラスタ頑健標準誤差の計算にsandwitchパッケージのvcovCL()関数を使っています。
fit1 <- lm(gamesecond ~ cm_dummy, data = md, weights = weights) coeftest(fit1, vcov. = vcovCL, cluster = ~subclass) coefci(fit1, vcov. = vcovCL, cluster = ~subclass)
t test of coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3001.47 289.44 10.3699 <2e-16 ***
cm_dummy 305.57 629.78 0.4852 0.6275
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
2.5 % 97.5 % (Intercept) 2434.1095 3568.831 cm_dummy -928.9141 1540.061
シンプルな線形回帰との違いは、重みを利用しているところと、誤差や信頼区間の計算にクラスタ頑健標準誤差を利用しているところです。マッチングでは似たサンプルをマッチさせるので、通常の計算方法で仮定している均一分散かつ無相関が成立しにくく標準誤差が過小評価されやすくなります。同一ペアの誤差は相関が高くクラスタを形成していると考えられるので、このような誤差構造に対応しているクラスタ頑健標準誤差を使っています。vcovCL()のクラスタ頑健誤差にはH0からH3までの種類を指定できますが、マッチングが適切にできていればペアの数が極端に少なくなることは稀なのでデフォルトのH1を使っています。
処置変数の係数の推定値がATEに対応しています。この例ではcm_dummyの係数の推定値がATEです。また、Interceptは対照群の結果の推定値に対応しています。
結果変数の回帰モデルに共変量を含める場合は次のように推定します。
md_cen <- md md_cen[cov_names] <- scale(md_cen[cov_names], scale = FALSE) fit2 <- lm(formula(str_c("gamesecond ~ cm_dummy * (", str_c(cov_names, collapse = "+"), ")")), data = md_cen, weights = weights) coeftest(fit2, vcov. = vcovCL, cluster = ~subclass)[1:2,] coefci(fit2, vcov. = vcovCL, cluster = ~subclass)[1:2,]
Estimate Std. Error t value Pr(>|t|) (Intercept) 2877.7969 273.2930 10.5300792 8.576712e-26 cm_dummy 489.2282 701.6637 0.6972402 4.856688e-01
2.5 % 97.5 % (Intercept) 2342.0873 3413.506 cm_dummy -886.1746 1864.631
バランシングで使った共変量をそのままモデルに含め、定数項と処置変数以外の回帰係数については解釈を行いません。また、marginal effectを計算するため中心化したデータを使っています。結果変数の回帰モデルに共変量を含めることでマッチング後も残っている不均衡が改善されると考えられるので、基本的には共変量を使った推定結果のほうを重視します。
因果効果の推定
ここから推定結果を得る一連の流れを説明します。まずマッチングと推定を行い複数の推定結果を得ます。共変量のバランスと推定値の関係からモデル依存性が低下しているかを確認し、モデル依存性が低下している推定結果に基づいて結果の解釈を行います。
マッチング
どのような手法やモデルを使うと適切なバランシングができるかわかりませんし、バランスの悪さがどのぐらい推定に影響を与えるのかもわかりません。そこで、複数の手法やモデルでバランシングと推定を行います。簡単なモデルではバランシングが十分でないこともあるので試行錯誤が必要なことも多いです。少なくともdistance、caliper、formulaの3つにはいくつかの異なる設定を試みたほうがよいでしょう。
MatchItで使えるdistanceはマハラノビス距離以外は全て傾向スコアですが、マッチングに傾向スコアを利用する場合は注意が必要です。(King & Nielsen, 2019)では、傾向スコアではブロックなしのランダム化を近似しているためマッチングで使うと、不均衡やモデル依存性、バイアス増加などを招くことを指摘しています。傾向スコアが近いサンプル同士でも共変量が類似しているとは限らないので、最適なマッチングがしにくいということです。そのため、基本的には傾向スコア以外でマッチングしたほうがよいと考えられます。傾向スコアマッチングの結果を最終的に採用する場合はマッチングが適切であるか入念な検証が必要になります。傾向スコアマッチングが必ず失敗するわけではないので、本記事では参考のため傾向スコアを利用したマッチングも行いますが、基本的にマハラノビス距離の結果を採用します。なお、この論文についてはこちらやこちらに解説記事があります。またKingによる解説動画には論文には掲載されていない例や図が紹介されていて理解が深まると思います。
複数の手法やモデルを使ってバランシングや推定を行う場合、Rユーザーであればtidyverseやpurrrを利用することが多いでしょう。ここではpurrrとほぼ同じコードで並列実行が可能なfurrrを利用し、計算に時間がかかるマッチングの実行を並列処理します。
ここではdistanceにマハラノビス距離とロジスティック回帰による傾向スコアを使い、caliperはTVwatch_dayに0.1刻みで0.1から0.5を設定し、formulaには下記コードで指定されている10種類を設定します。TVwatch_dayのみにcaliperを設定しているのは、TVwatch_dayがもっともバランスが悪いためです。formulaで指定しているモデルは、バランスが悪い共変量の2乗や交互作用項を入れることで、これらのバランスを改善することを意図したものになっています。
マッチングを行うコードは以下のとおりです。設定値の組み合わせを作り、その設定に基づいてmatchit()を実行し得られたオブジェクトをmt_obj列に入れます。そのため、各行に各設定で実行したマッチング結果のオブジェクトが入っています。さらに、そのオブジェクトから得られるsummary()の結果をmt_smmry列に入れ、bal.tab()の結果をcblt_smmry列に入れています。また、各行がどのような設定になっているかを簡単に見れるようにするためname列に設定の組み合わせの名前を入れています。このようにすることで各設定のマッチング結果やバランシング結果を容易に抽出できます。
# caliperの設定(ここではTVwatch_dayのみ) caliper_settings <- map(seq(0.1, 0.5, 0.1), ~ { v <- c(.) names(v) <- "TVwatch_day" v}) names(caliper_settings) <- str_c("c", as.character(seq(0.1, 0.5, 0.1))) caliper_settings <- c(caliper_settings, list(cNULL = c(TVwatch_day = -1))) # distanceの設定 distance_settings <- c("glm", "mahalanobis") # モデルの設定 lt_base_str <- str_c("(", str_c(cov_names, collapse = "+"), ")") # 共変量の和(元記事と同じ) cov_names2 <- c(cov_names, c("T", "F1", "F2", "F3", "M1", "M2", "M3")) # 視聴者層を追加 lt_str <- str_c("(", str_c(cov_names2, collapse = "+"), ")") # 共変量の和(視聴者層を追加) formula_settings <- c( str_c("cm_dummy ~ ", lt_base_str), str_c("cm_dummy ~ ", lt_str), str_c("cm_dummy ~ I(TVwatch_day^2) + ", lt_str), str_c("cm_dummy ~ TVwatch_day * (TVwatch_day + area_keihanshin) + ", lt_str), str_c("cm_dummy ~ TVwatch_day * (TVwatch_day + age + inc + area_keihanshin) + ", lt_str), str_c("cm_dummy ~ (TVwatch_day + age + inc + area_keihanshin) * (TVwatch_day + age + inc + area_keihanshin) + ", lt_str), str_c("cm_dummy ~ (", str_c(cov_names2, collapse = "+"), ")*TVwatch_day"), str_c("cm_dummy ~ (", str_c(cov_names2, collapse = "+"), ")*area_keihanshin"), str_c("cm_dummy ~ (", str_c(cov_names2, collapse = "+"), ")*(TVwatch_day + area_keihanshin)"), str_c("cm_dummy ~ (", str_c(cov_names2, collapse = "+"), ")*(TVwatch_day + age + inc + area_keihanshin)") ) %>% map(formula) names(formula_settings) <- str_c("f", str_pad(1:length(formula_settings), 2, pad = 0)) # バランス確認の関数 bal_tab_obj <- function(obj) { bal.tab(obj, s.d.denom = "pooled", disp = c("means", "sds"), stats = c("mean.diffs", "variance.ratios", "ks.statistics"), thresholds = c(m = 0.1, v = 2)) } # マッチング実行の関数 exec_matching <- function(dat, distance_settings, caliper_settings, formula_settings, estimand = "ATE", method = "full", n_worker = 8) { # furrrの設定 plan(multisession, workers = n_worker) # 設定の組み合わせ crossing(distance = distance_settings, caliper = caliper_settings, formula = formula_settings) %>% bind_cols( # 設定名 crossing( distance = distance_settings, caliper = names(caliper_settings), formula = names(formula_settings) ) %>% mutate(name = str_c(distance, caliper, formula, sep = "_")) %>% dplyr::select(name) ) %>% mutate(mt_obj = future_pmap(list(distance, caliper, formula), function(distance, caliper, formula) { if (any(caliper < 0)) { caliper_ <- NULL } else { caliper_ <- caliper } matchit( formula = formula, data = dat, estimand = estimand, method = method, distance = distance, caliper = caliper_ ) }, .options = furrr_options(seed = TRUE))) %>% mutate(mt_smmry = map(mt_obj, ~ summary(.))) %>% mutate(cblt_smmry = map(mt_obj, ~ bal_tab_obj(.))) } # マッチングの実行 df_mbal <- exec_matching(df_ds3, distance_settings, caliper_settings, formula_settings)
次に、マッチング結果のバランスの傾向を見るため、一部のデータを抽出してまとめ直します。ここではSMDの最大値と平均値、SMDが0.1以上の共変量の数、マッチしなかったサンプル数、ペア同士の差の最大値と平均値を抽出しています。
# バランス指標抽出関数 summary_matching_balance <- function(dat) { dat %>% mutate(cblt_tbl = map(cblt_smmry, ~ .$Balance), cblt_obs = map(cblt_smmry, ~ .$Observations)) %>% mutate( max_smd = map(cblt_tbl, ~ tibble(max_smd = max(abs(.$Diff.Adj)))), mean_smd = map(cblt_tbl, ~ tibble(mean_smd = mean(abs(.$Diff.Adj)))), n_unbalance = map(cblt_tbl, ~ tibble(n_unbalance = sum(abs(.$Diff.Adj) >= 0.1))), n_unmatched = map(cblt_obs, ~ {.[rownames(.) == "Unmatched",]}), max_std_pair_dist = map(mt_smmry, ~ tibble(max_std_pair_dist = max(.$sum.matched[,"Std. Pair Dist."]))), mean_std_pair_dist = map(mt_smmry, ~ tibble(mean_std_pair_dist = mean(.$sum.matched[,"Std. Pair Dist."]))) ) %>% dplyr::select(name, max_smd, mean_smd, n_unbalance, n_unmatched, max_std_pair_dist, mean_std_pair_dist) %>% unnest(max_smd) %>% unnest(mean_smd) %>% unnest(n_unbalance) %>% unnest(n_unmatched) %>% rename(n_unmatched_ctr = Control, n_unmatched_tr = Treated) %>% unnest(max_std_pair_dist) %>% unnest(mean_std_pair_dist) } df_mbal_summary <- summary_matching_balance(df_mbal) df_mbal_summary %>% filter(max_smd < 0.1) %>% kable()
| name | max_smd | mean_smd | n_unbalance | n_unmatched_ctr | n_unmatched_tr | max_std_pair_dist | mean_std_pair_dist |
|---|---|---|---|---|---|---|---|
| glm_c0.2_f08 | 0.0924526 | 0.0239487 | 0 | 0 | 60 | 1.0663395 | 0.6266124 |
| glm_c0.3_f05 | 0.0893715 | 0.0281436 | 0 | 0 | 45 | 1.0617177 | 0.6132495 |
| glm_c0.3_f09 | 0.0554426 | 0.0224114 | 0 | 0 | 45 | 1.0645776 | 0.6324145 |
| glm_c0.4_f02 | 0.0886711 | 0.0177467 | 0 | 0 | 37 | 1.1193090 | 0.6316043 |
| glm_c0.4_f03 | 0.0886711 | 0.0177467 | 0 | 0 | 37 | 1.1193090 | 0.6316043 |
| glm_c0.4_f04 | 0.0990389 | 0.0208258 | 0 | 0 | 37 | 1.1082732 | 0.6225565 |
| glm_c0.4_f05 | 0.0830745 | 0.0261869 | 0 | 0 | 37 | 1.0439178 | 0.6277055 |
| glm_c0.4_f06 | 0.0783583 | 0.0223644 | 0 | 0 | 37 | 1.0530267 | 0.6142931 |
| glm_c0.4_f09 | 0.0482493 | 0.0189923 | 0 | 0 | 37 | 1.0861440 | 0.6367170 |
| glm_c0.5_f02 | 0.0699400 | 0.0175528 | 0 | 0 | 23 | 1.1483252 | 0.6386019 |
| glm_c0.5_f03 | 0.0699400 | 0.0175528 | 0 | 0 | 23 | 1.1483252 | 0.6386019 |
| glm_c0.5_f04 | 0.0687159 | 0.0182210 | 0 | 0 | 23 | 1.1412132 | 0.6329054 |
| glm_c0.5_f06 | 0.0658810 | 0.0212731 | 0 | 0 | 23 | 1.0150644 | 0.6110976 |
| glm_c0.5_f09 | 0.0593807 | 0.0198482 | 0 | 0 | 23 | 1.0871745 | 0.6475080 |
| glm_cNULL_f01 | 0.0838053 | 0.0222311 | 0 | 0 | 0 | 1.1421366 | 0.6582768 |
| glm_cNULL_f02 | 0.0616028 | 0.0185624 | 0 | 0 | 0 | 1.1601744 | 0.6778365 |
| glm_cNULL_f03 | 0.0616028 | 0.0185624 | 0 | 0 | 0 | 1.1601744 | 0.6778365 |
| glm_cNULL_f04 | 0.0532585 | 0.0164868 | 0 | 0 | 0 | 1.1696635 | 0.6742358 |
| glm_cNULL_f05 | 0.0881802 | 0.0243057 | 0 | 0 | 0 | 1.1197885 | 0.6725867 |
| glm_cNULL_f06 | 0.0753675 | 0.0178894 | 0 | 0 | 0 | 1.0492625 | 0.6451546 |
| glm_cNULL_f07 | 0.0703572 | 0.0190716 | 0 | 0 | 0 | 1.0713330 | 0.6285979 |
| mahalanobis_c0.4_f08 | 0.0950025 | 0.0309073 | 0 | 0 | 37 | 0.9669033 | 0.4530344 |
| mahalanobis_c0.5_f08 | 0.0955574 | 0.0300822 | 0 | 0 | 23 | 0.9639724 | 0.4456287 |
SMDが0.1以下のものを見ると傾向スコアを使ったものが多いことがわかります。ただし、マハラノビス距離と比較すると、SMDが小さいにも関わらずペア同士の差が大きい傾向があることがわかります。またcaliperでマッチしなくなるサンプルは処置ありのほうのみに生じていることがわかります。サンプル数は全体で1万なので、マッチしなくなるサンプル数は全体の1%未満です。
推定
次にこれらのマッチング結果からATEの推定値を計算します。推定コードは以下のとおりです。
centered <- function(dat, covnames) { dat_cen <- dat dat_cen[covnames] <- scale(dat_cen[covnames], scale = FALSE) dat_cen } # ATE推定の関数 estimate_ate_after_fullmatching <- function(obj, dat, outcome_name, treat_name, covnames) { lm_w <- function(dat, f) { lm(f, data = dat, weights = weights) } coeftest_tidy <- function(fit, dat, tr_name) { coeftest(fit, vcov. = vcovCL, cluster = dat$subclass) %>% tidy() %>% filter(term %in% c("(Intercept)", tr_name)) %>% mutate(term = c("E0", "ATE")) } coefci_tidy <- function(fit, dat, tr_name) { d <- coefci(fit, vcov. = vcovCL, cluster = dat$subclass) %>% data.frame() d <- d[rownames(d) %in% c("(Intercept)", tr_name),] colnames(d) <- c("ci2.5", "ci97.5") d %>% mutate(ci_name = c("E0", "ATE")) } centered_covnames <- covnames formula_wo <- formula(str_c(outcome_name, "~", treat_name)) formula_w <- formula(str_c(outcome_name, "~", treat_name, " * (", str_c(centered_covnames, collapse = "+"), ")")) obj %>% mutate(md = map(.x = mt_obj, .f = match.data, data = dat)) %>% mutate(fit_wo_ca = map(.x = md, .f = lm_w, f = formula_wo)) %>% mutate(ate_est_wo_ca = map2(.x = fit_wo_ca, .y = md, .f = coeftest_tidy, tr_name = treat_name)) %>% mutate(ate_ci_wo_ca = map2(.x = fit_wo_ca, .y = md, .f = coefci_tidy, tr_name = treat_name)) %>% mutate(md_cen = map(.x = md, .f = centered, covnames = centered_covnames)) %>% mutate(fit_w_ca = map(.x = md_cen, .f = lm_w, f = formula_w)) %>% mutate(ate_est_w_ca = map2(.x = fit_w_ca, .y = md_cen, .f = coeftest_tidy, tr_name = treat_name)) %>% mutate(ate_ci_w_ca = map2(.x = fit_w_ca, .y = md_cen, .f = coefci_tidy, tr_name = treat_name)) } # ATE推定 df_mbal <- estimate_ate_after_fullmatching(df_mbal, df_ds3, "gamesecond", "cm_dummy", cov_names2)
マッチングのときと同様に一部のデータを抽出して推定結果の傾向を見ます。ここでは共変量による再調整なしとありの双方について、推定値と標準誤差、p値、95%信頼区間を抽出します。共変量による再調整なしには末尾に"wo"、ありには"w"をつけています。また、バランシングのサマリと結合することでバランスと推定値の関係を調べやすくします。
summary_ate_estimation <- function(dat, df_balance_summary) { dat %>% dplyr::select(name) %>% bind_cols( dat %>% unnest(ate_est_wo_ca) %>% filter(term == "ATE") %>% dplyr::select(estimate, std.error, p.value) %>% rename(estimate_wo = estimate, std.error_wo = std.error, p.value_wo = p.value) ) %>% bind_cols( dat %>% unnest(ate_ci_wo_ca) %>% filter(ci_name == "ATE") %>% dplyr::select(ci2.5, ci97.5) %>% rename(ci2.5_wo = ci2.5, ci97.5_wo = ci97.5) ) %>% bind_cols( dat %>% unnest(ate_est_w_ca) %>% filter(term == "ATE") %>% dplyr::select(estimate, std.error, p.value) %>% rename(estimate_w = estimate, std.error_w = std.error, p.value_w = p.value) ) %>% bind_cols( dat %>% unnest(ate_ci_w_ca) %>% filter(ci_name == "ATE") %>% dplyr::select(ci2.5, ci97.5) %>% rename(ci2.5_w = ci2.5, ci97.5_w = ci97.5) ) %>% mutate(abs_diff_est = abs(estimate_wo - estimate_w)) %>% bind_cols(df_balance_summary %>% dplyr::select(-name)) } df_mbal_est_summary <- summary_ate_estimation(df_mbal, df_mbal_summary) df_mbal_est_summary %>% filter(max_smd < 0.1) %>% kable()
| name | estimate_wo | std.error_wo | p.value_wo | ci2.5_wo | ci97.5_wo | estimate_w | std.error_w | p.value_w | ci2.5_w | ci97.5_w | abs_diff_est | max_smd | mean_smd | n_unbalance | n_unmatched_ctr | n_unmatched_tr | max_std_pair_dist | mean_std_pair_dist |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| glm_c0.1_f06 | -248.97800 | 641.5127 | 0.6979424 | -1506.474 | 1008.5176 | 238.77251 | 659.5738 | 0.7173521 | -1054.12738 | 1531.6724 | 487.75051 | 0.0984415 | 0.0266279 | 0 | 0 | 104 | 1.0607110 | 0.5871656 |
| glm_c0.2_f06 | -312.82333 | 560.8631 | 0.5770253 | -1412.229 | 786.5819 | 53.86054 | 583.3530 | 0.9264383 | -1089.63044 | 1197.3515 | 366.68387 | 0.0858986 | 0.0200395 | 0 | 0 | 60 | 1.0835793 | 0.5937371 |
| glm_c0.2_f08 | -694.27948 | 638.2405 | 0.2767087 | -1945.360 | 556.8012 | -427.91348 | 705.6728 | 0.5442692 | -1811.17613 | 955.3492 | 266.36600 | 0.0924526 | 0.0239487 | 0 | 0 | 60 | 1.0663395 | 0.6266124 |
| glm_c0.3_f05 | 670.11019 | 1393.2463 | 0.6305481 | -2060.935 | 3401.1549 | 532.64914 | 747.2290 | 0.4759662 | -932.07187 | 1997.3701 | 137.46105 | 0.0893715 | 0.0281436 | 0 | 0 | 45 | 1.0617177 | 0.6132495 |
| glm_c0.3_f06 | -352.49966 | 743.0294 | 0.6352188 | -1808.988 | 1103.9882 | -91.70053 | 657.2528 | 0.8890413 | -1380.04991 | 1196.6488 | 260.79913 | 0.0889126 | 0.0194738 | 0 | 0 | 45 | 1.1123080 | 0.6034775 |
| glm_c0.3_f09 | -189.15990 | 588.3389 | 0.7478268 | -1342.423 | 964.1035 | 13.53318 | 607.9403 | 0.9822404 | -1178.15368 | 1205.2200 | 202.69309 | 0.0554426 | 0.0224114 | 0 | 0 | 45 | 1.0645776 | 0.6324145 |
| glm_c0.4_f02 | 353.96028 | 1243.1621 | 0.7758602 | -2082.889 | 2790.8094 | 366.62701 | 715.9869 | 0.6086216 | -1036.85300 | 1770.1070 | 12.66673 | 0.0886711 | 0.0177467 | 0 | 0 | 37 | 1.1193090 | 0.6316043 |
| glm_c0.4_f04 | 682.72424 | 1363.5947 | 0.6166076 | -1990.197 | 3355.6456 | 636.75840 | 732.2081 | 0.3845175 | -798.51836 | 2072.0352 | 45.96583 | 0.0990389 | 0.0208258 | 0 | 0 | 37 | 1.1082732 | 0.6225565 |
| glm_c0.4_f05 | 739.00860 | 1241.7864 | 0.5517786 | -1695.144 | 3173.1610 | 778.20192 | 772.3249 | 0.3136665 | -735.71197 | 2292.1158 | 39.19331 | 0.0830745 | 0.0261869 | 0 | 0 | 37 | 1.0439178 | 0.6277055 |
| glm_c0.4_f06 | -197.52508 | 785.3521 | 0.8014239 | -1736.974 | 1341.9237 | 150.24611 | 654.2391 | 0.8183684 | -1132.19569 | 1432.6879 | 347.77119 | 0.0926864 | 0.0197675 | 0 | 0 | 37 | 1.1395282 | 0.6209101 |
| glm_c0.4_f09 | -53.84889 | 593.1827 | 0.9276695 | -1216.607 | 1108.9091 | 188.26027 | 616.1724 | 0.7599676 | -1019.56301 | 1396.0836 | 242.10916 | 0.0482493 | 0.0189923 | 0 | 0 | 37 | 1.0861440 | 0.6367170 |
| glm_c0.5_f02 | -89.70513 | 1093.7716 | 0.9346368 | -2233.718 | 2054.3080 | 114.32914 | 767.9303 | 0.8816517 | -1390.97024 | 1619.6285 | 204.03427 | 0.0699400 | 0.0175528 | 0 | 0 | 23 | 1.1483252 | 0.6386019 |
| glm_c0.5_f04 | 224.27774 | 1201.6539 | 0.8519460 | -2131.206 | 2579.7619 | 355.57446 | 787.6177 | 0.6516710 | -1188.31622 | 1899.4651 | 131.29672 | 0.0687159 | 0.0182210 | 0 | 0 | 23 | 1.1412132 | 0.6329054 |
| glm_c0.5_f06 | -791.73472 | 527.3405 | 0.1332908 | -1825.428 | 241.9590 | -452.07506 | 547.0942 | 0.4086423 | -1524.49088 | 620.3408 | 339.65967 | 0.0848999 | 0.0199176 | 0 | 0 | 23 | 1.1364163 | 0.6315888 |
| glm_c0.5_f09 | 802.19627 | 866.8471 | 0.3547707 | -896.999 | 2501.3916 | 1091.16771 | 814.0556 | 0.1801430 | -504.54660 | 2686.8820 | 288.97144 | 0.0593807 | 0.0198482 | 0 | 0 | 23 | 1.0871745 | 0.6475080 |
| glm_cNULL_f01 | 5528.15105 | 4999.4959 | 0.2688649 | -4271.867 | 15328.1694 | 2037.12794 | 1063.0116 | 0.0553461 | -46.59013 | 4120.8460 | 3491.02311 | 0.0838053 | 0.0222311 | 0 | 0 | 0 | 1.1421366 | 0.6582768 |
| glm_cNULL_f02 | -488.91451 | 781.9185 | 0.5318045 | -2021.632 | 1043.8032 | -152.92377 | 684.1301 | 0.8231274 | -1493.95742 | 1188.1099 | 335.99074 | 0.0616028 | 0.0185624 | 0 | 0 | 0 | 1.1601744 | 0.6778365 |
| glm_cNULL_f04 | 415.46879 | 1256.0726 | 0.7408266 | -2046.686 | 2877.6240 | 393.06214 | 785.9929 | 0.6170273 | -1147.64312 | 1933.7674 | 22.40665 | 0.0532585 | 0.0164868 | 0 | 0 | 0 | 1.1696635 | 0.6742358 |
| glm_cNULL_f05 | 660.31034 | 1251.2300 | 0.5976992 | -1792.352 | 3112.9730 | 431.03591 | 803.1657 | 0.5915068 | -1143.33161 | 2005.4034 | 229.27442 | 0.0881802 | 0.0243057 | 0 | 0 | 0 | 1.1197885 | 0.6725867 |
| glm_cNULL_f07 | 7182.64188 | 6904.8897 | 0.2982603 | -6352.332 | 20717.6155 | 1670.28248 | 1127.0849 | 0.1383855 | -539.03216 | 3879.5971 | 5512.35941 | 0.0703572 | 0.0190716 | 0 | 0 | 0 | 1.0713330 | 0.6285979 |
| mahalanobis_c0.4_f08 | -182.27715 | 548.7708 | 0.7397789 | -1257.979 | 893.4245 | -133.27053 | 534.5764 | 0.8031330 | -1181.14906 | 914.6080 | 49.00662 | 0.0950025 | 0.0309073 | 0 | 0 | 37 | 0.9669033 | 0.4530344 |
| mahalanobis_c0.5_f08 | -315.56045 | 529.1341 | 0.5509407 | -1352.770 | 721.6492 | -292.80174 | 503.4200 | 0.5608324 | -1279.60721 | 694.0037 | 22.75871 | 0.0955574 | 0.0300822 | 0 | 0 | 23 | 0.9639724 | 0.4456287 |
いずれのケースでも信頼区間に0が含まれていることがわかります。SMDが基準を満たしていても推定値にばらつきがあるので、どのぐらいの推定値が妥当なのかを検討していきます。"glm_cNULL_f01"や"glm_cNULL_f07"のように傾向スコアでは標準誤差が他と比較して非常に大きいケースがあるので、それらは検討対象から除外します。
結果の検証
まずSMDの最大値と推定値の関係を調べてみましょう。バランスがとれるほどモデル依存性が低下するので推定値も安定すると考えられます。どのぐらいバランスがとれればモデル依存性が十分低下するかはデータによるので、複数の推定結果について調べる必要があります。
SMDの最大値と推定値の関係をプロットすると以下のようになります。なお、標準誤差が異常に大きいケースは除外しています。
df_mbal_est_summary_ <- df_mbal_est_summary %>% bind_cols(df_mbal %>% dplyr::select(distance)) df_mbal_est_summary_ %>% filter(std.error_w <= 2000) %>% ggplot(aes(x = max_smd, y = estimate_w, group = distance, color = distance)) + geom_point()

マハラノビス距離ではSMDの最大値が小さくなるほど推定値のばらつきが小さくなっておりモデル依存性が低くなっていると考えられます。SMDの最大値が0.15を下回ったあたりから、推定値は-400から100程度になっています。一方で、傾向スコアではSMDと推定値に明瞭な関係性は見られないのでモデル依存性が残っている可能性が高いと考えられます。このことからマハラノビス距離の推定結果を採用したほうがよいと判断できます。信頼区間も表示させると以下のようになります。
df_mbal_est_summary_ %>% filter(std.error_w <= 2000) %>% ggplot(aes(x = max_smd, y = estimate_w, group = distance, color = distance)) + geom_errorbar(aes(ymax = ci97.5_w, ymin = ci2.5_w)) + geom_point()

バランスが比較的よいときでも信頼区間の幅がおよそ2000以上となっており、全体的に誤差が大きいことが視覚的にも確認できます。SMDの最大値が0.15以下のマハラノビス距離の結果のみを表示すると以下のようになります。
df_mbal_est_summary_ %>% filter(distance == "mahalanobis", max_smd <= 0.15) %>% ggplot(aes(x = max_smd, y = estimate_w, group = distance, color = distance)) + geom_errorbar(aes(ymax = ci97.5_w, ymin = ci2.5_w)) + geom_point()

推定値だけを見るとSMDの最大値が0.1付近のマハラノビス距離の結果の中にはATEが負のケースが多く、CM視聴があるとアプリ利用時間が減少するという奇妙な結果になっています。しかし、信頼区間まで確認すると、効果がマイナスと捉えるより誤差によって偶然マイナスの結果が得られたと考えるほうが自然であることがわかります。
結果を一つだけ報告する必要があるならば、今回の場合、マハラノビス距離でSMDの最大値が一番小さくなった"mahalanobis_c0.4_f08"を使うのがよいでしょう。共変量による再調整をしたときの推定値を使うと、CM視聴の効果は-133、信頼区間は-1181から915となります。CM視聴によるアプリ利用時間への効果は確認できなかったという結論になります。
今回はCM視聴によるアプリ利用時間の効果しか推定していないのでこれ以上のことはわかりませんが、この結果を起点として分析方針を考えることでCM視聴の効果を明らかにするのに役立つはずです。CMの内容が認知を目的としたものならば既存ユーザーの利用頻度や利用時間への影響はほとんどないですし、キャンペーン告知など利用促進を目的としたものならば影響はあるはずです。認知目的であれば新規ユーザーの獲得や利用定着が不十分な可能性が考えられます。CM視聴によってアプリが認知されれば新規ユーザーは増えそうです。しかし、新規ユーザーを獲得できたとしても、新規ユーザー数が少ないもしくは利用時間が短い場合は全体のアプリ利用時間への寄与は小さいので効果は確認できません。一方で利用促進が目的であれば利用時間が増えたユーザー数、利用頻度、1回あたりの利用時間への効果が不十分であった可能性が考えられます。
念のため"mahalanobis_c0.4_f08"の共変量のバランスを確認しておきましょう。
df_mbal %>% filter(name == "mahalanobis_c0.4_f08") %>% pull(cblt_smmry)
[[1]]
Call
matchit(formula = formula, data = df_ds3, method = "full", distance = distance,
estimand = "ATE", caliper = caliper_)
Balance Measures
Type M.0.Adj SD.0.Adj M.1.Adj SD.1.Adj Diff.Adj M.Threshold V.Ratio.Adj V.Threshold KS.Adj
TVwatch_day Contin. 7741.0652 7396.3788 8262.3811 7326.1776 0.0701 Balanced, <0.1 0.9811 Balanced, <2 0.0943
age Contin. 41.1833 10.4302 40.3085 10.5230 -0.0842 Balanced, <0.1 1.0179 Balanced, <2 0.0312
sex Binary 0.6589 . 0.6437 . -0.0152 Balanced, <0.1 . 0.0152
marry_dummy Binary 0.6476 . 0.6173 . -0.0303 Balanced, <0.1 . 0.0303
child_dummy Binary 0.3951 . 0.3828 . -0.0123 Balanced, <0.1 . 0.0123
inc Contin. 361.4717 264.4669 342.8220 262.8835 -0.0697 Balanced, <0.1 0.9881 Balanced, <2 0.0398
pmoney Contin. 3.4989 3.2643 3.5075 3.3467 0.0026 Balanced, <0.1 1.0512 Balanced, <2 0.0268
area_kanto Binary 0.0664 . 0.1146 . 0.0483 Balanced, <0.1 . 0.0483
area_tokai Binary 0.1654 . 0.0704 . -0.0950 Balanced, <0.1 . 0.0950
area_keihanshin Binary 0.2159 . 0.1824 . -0.0335 Balanced, <0.1 . 0.0335
job_dummy1 Binary 0.5901 . 0.5491 . -0.0410 Balanced, <0.1 . 0.0410
job_dummy2 Binary 0.0736 . 0.0563 . -0.0173 Balanced, <0.1 . 0.0173
job_dummy3 Binary 0.0567 . 0.0683 . 0.0115 Balanced, <0.1 . 0.0115
job_dummy4 Binary 0.0141 . 0.0101 . -0.0040 Balanced, <0.1 . 0.0040
job_dummy5 Binary 0.1014 . 0.1305 . 0.0292 Balanced, <0.1 . 0.0292
job_dummy6 Binary 0.0908 . 0.1024 . 0.0117 Balanced, <0.1 . 0.0117
job_dummy7 Binary 0.0395 . 0.0592 . 0.0197 Balanced, <0.1 . 0.0197
fam_str_dummy1 Binary 0.1483 . 0.2130 . 0.0647 Balanced, <0.1 . 0.0647
fam_str_dummy2 Binary 0.1475 . 0.1608 . 0.0133 Balanced, <0.1 . 0.0133
fam_str_dummy3 Binary 0.6042 . 0.5675 . -0.0367 Balanced, <0.1 . 0.0367
fam_str_dummy4 Binary 0.0813 . 0.0462 . -0.0351 Balanced, <0.1 . 0.0351
T Binary 0.0117 . 0.0124 . 0.0007 Balanced, <0.1 . 0.0007
F1 Binary 0.1246 . 0.1081 . -0.0165 Balanced, <0.1 . 0.0165
F2 Binary 0.1559 . 0.1875 . 0.0316 Balanced, <0.1 . 0.0316
F3 Binary 0.0565 . 0.0510 . -0.0055 Balanced, <0.1 . 0.0055
M1 Binary 0.1400 . 0.1678 . 0.0278 Balanced, <0.1 . 0.0278
M2 Binary 0.3482 . 0.3218 . -0.0264 Balanced, <0.1 . 0.0264
M3 Binary 0.1630 . 0.1514 . -0.0116 Balanced, <0.1 . 0.0116
Balance tally for mean differences
count
Balanced, <0.1 28
Not Balanced, >0.1 0
Variable with the greatest mean difference
Variable Diff.Adj M.Threshold
area_tokai -0.095 Balanced, <0.1
Balance tally for variance ratios
count
Balanced, <2 4
Not Balanced, >2 0
Variable with the greatest variance ratio
Variable V.Ratio.Adj V.Threshold
pmoney 1.0512 Balanced, <2
Sample sizes
Control Treated
All 5856. 4144.
Matched (ESS) 1681.95 707.92
Matched (Unweighted) 5856. 4107.
Unmatched 0. 37.
共変量の分布についても確認しましょう。SMDが小さくとも分布が異なることはあります。分布の差はKS統計量でわかるので、共変量の数が多い場合はKS統計量が大きいものを中心に確認するのがよいと思います。ここではKS統計量が大きいarea_tokai、TVwatch_day、fam_str_dummy1の3つについて見てみます。
bal_plot_hist <- function(obj, var_name) { bal.plot(obj, var.name = var_name, which = "both", type = "histogram", mirror = TRUE) } mt_obj <- df_mbal %>% filter(name == "mahalanobis_c0.4_f08") %>% pull(mt_obj) %>% .[[1]] bal_plot_hist(mt_obj, "area_tokai") bal_plot_hist(mt_obj, "TVwatch_day") bal_plot_hist(mt_obj, "fam_str_dummy1")
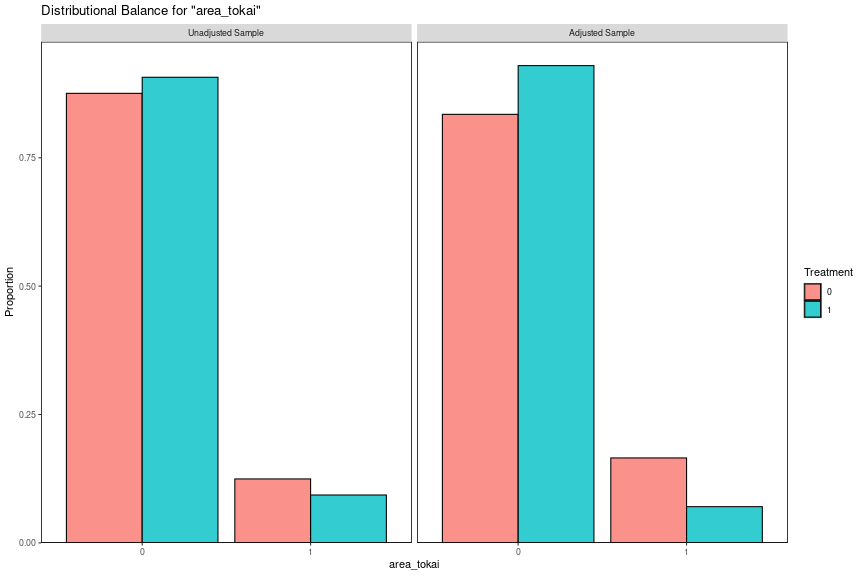
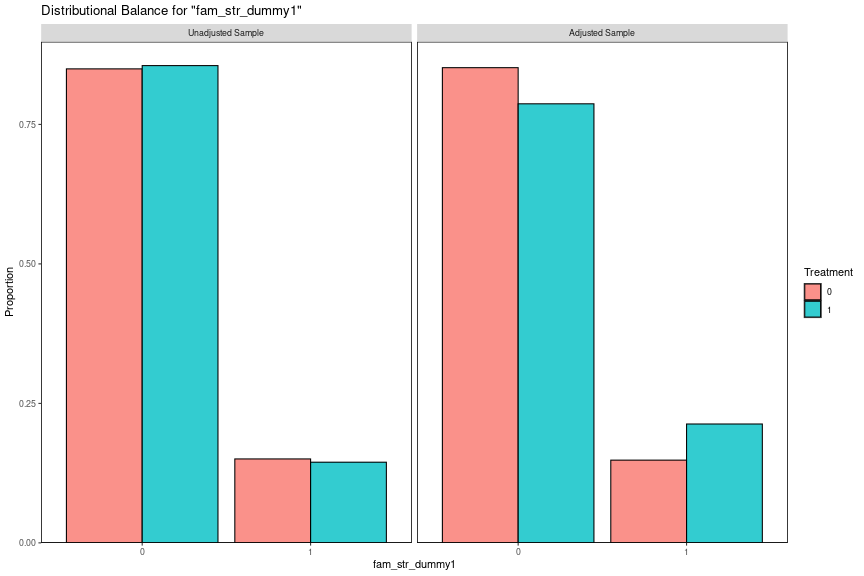
area_tokaiは偏りが大きめですが結果への影響が比較的小さいので推定値が大幅に変わることはないと考えられます。
なお、バランシングがうまくいっても推定値が大きくばらつく場合、観測共変量との相関が小さくかつ結果に大きく影響する未観測の共変量が存在する可能性が考えられます。共変量のバランシングによって未観測共変量の影響が小さくなるのは、観測共変量と未観測共変量との間に相関があることが多いためです。もし未観測の重要共変量が観測共変量と独立である場合は、共変量のバランシングをしても未観測共変量によるバイアスは小さくなりません。この場合、本記事で扱っている共変量のバランシングでは適切な推定は困難です。
ここからは共変量のバランスと、マッチング後の再調整および標準誤差との関係を見てみましょう。
SMDの最大値とATE推定時に共変量で再調整したときとしないときの差の関係を見てみましょう。マッチングで共変量のバランシングが十分にできているとATE推定時の再調整の影響は小さくなるはずです。
df_mbal_est_summary_ %>% filter(std.error_wo <= 2000) %>% ggplot(aes(x = max_smd, y = abs_diff_est, group = distance, color = distance)) + geom_point()

マハラノビス距離の結果を見ると、SMDの最大値が小さくなるとマッチング後の再調整による推定値の変化幅は小さくなる傾向が見られます。これはモデル依存性が低下していることを示していると考えられます。一方で、傾向スコアマッチングについてはそのような傾向は見られません。
次に共変量による再調整で標準誤差が縮小しているかを確認します。再調整なしの標準誤差と標準誤差の差分(再調整なし - 再調整あり)をプロットすると以下のようになります。
df_mbal_est_summary_ %>% filter(std.error_wo <= 2000) %>% mutate(diff_std.error = std.error_wo - std.error_w) %>% ggplot(aes(x = std.error_wo, y = diff_std.error, group = distance, color = distance)) + geom_point()
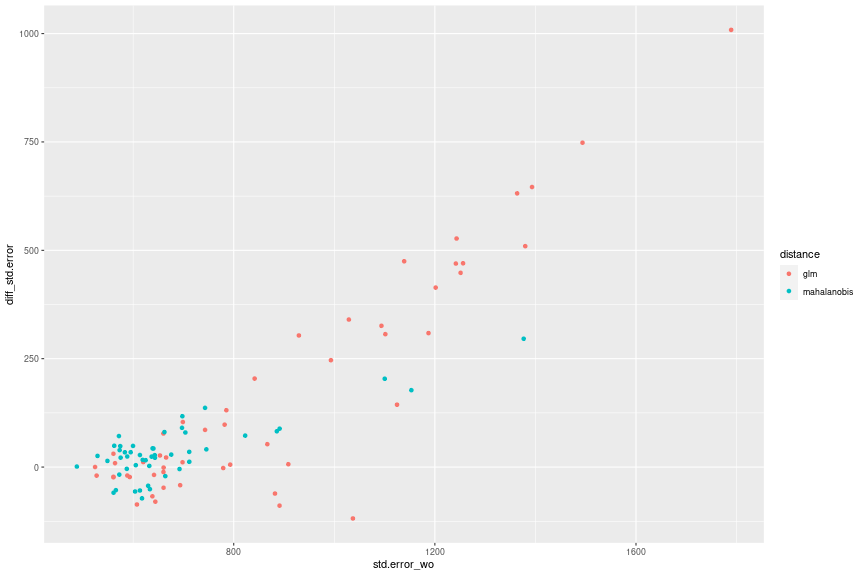
再調整なしの標準誤差が大きいほど、再調整によって標準誤差が縮小していることがわかります。一方で、再調整なしの標準誤差が相対的に小さいケース、具体的には700を下回ったあたりでは標準誤差の拡大が縮小と同程度生じていることがわかります。再調整によって必ずしも標準誤差が縮小するわけではなく、特に再調整なしの標準誤差が比較的小さいときは標準誤差が拡大しやすいことに注意したほうがよさそうです。
重み付け
重み付けにはWeightItパッケージを利用します。WeightItは重み付けで使われるパッケージの共通インターフェースを提供しており、複数の手法やモデルを使うのに適しています。なお、本記事ではInverse Probability Weighting(IPW、逆確率重み付け)しか使いませんが、WeightItにはIPW以外で重み付けする方法も含まれています。
最初にWeightItの使い方や推定方法を説明し、その後に推定結果を得る一連の流れを説明します。
WeightItの使い方
重み付け
まずWeightItの簡単な使い方を紹介します。weightit()関数のestimandに推定する種類、methodに重み付けの手法を指定します。ここではATEを計算するためestimandに"ATE"を指定し、ロジスティック回帰による傾向スコアを使うためmethodに"ps"を指定します。なお、WeightItが対応していないパッケージで計算した傾向スコアなども利用することができます。詳細はWeightItのvignettesをご参照ください。
W.out <- weightit( ds3_formula, data = df_ds3, estimand = "ATE", method = "ps") summary(W.out)
Summary of weights
- Weight ranges:
Min Max
treated 1.0020 |----| 19.0312
control 1.0212 |---------------------------| 91.1488
- Units with 5 greatest weights by group:
9921 9916 9914 9911 9910
treated 19.0269 19.028 19.0305 19.0308 19.0312
5428 4068 3390 2706 672
control 91.1353 91.1359 91.1414 91.1461 91.1488
- Weight statistics:
Coef of Var MAD Entropy # Zeros
treated 0.760 0.442 1.032 0
control 1.714 0.428 0.933 0
overall 1.312 0.457 0.980 0
- Effective Sample Sizes:
Control Treated
Unweighted 5856. 4144.
Weighted 1487.52 2626.6
summary()関数を使うと重みのサマリ情報を見ることができます。重みの幅で重みが大きすぎないかをチェックします。重みの変動が小さいと精度が高くなります。そのため変動係数"Coef of Var"や平均絶対偏差”MAD”、負のエントロピー"Entropy"は小さい方が望ましいです。"# Zeros"は重み0の数です。重みが0ということはサンプルデータを除外するのと同じことになるのでATEとは異なるものが推定される可能性があり注意が必要です。IPWでATEを推定する場合は重みの最小値は1なので気にする必要はないですが、IPW以外の重み付け手法を使うと重みが0になることがあるので注意が必要です。有効サンプルサイズは多いほどよいです。重みの変動が小さくなると有効サンプルサイズが増えます。
この例では対照群の重みの最大値が91と大きめで重みの変動係数も大きめであることがわかります。そのため、推定値のバイアスが大きくなりやすく標準誤差も大きくなりやすいと考えられます。
次にバランスについて確認します。マッチングの節で定義したbal_tab_obj()関数を使います。
bal_tab_obj(W.out)
Call
weightit(formula = ds3_formula, data = df_ds3, method = "ps",
estimand = "ATE")
Balance Measures
Type M.0.Adj SD.0.Adj M.1.Adj SD.1.Adj Diff.Adj M.Threshold V.Ratio.Adj V.Threshold KS.Adj
prop.score Distance 0.4558 0.2793 0.4299 0.2350 -0.1206 0.7081 Balanced, <2 0.0962
TVwatch_day Contin. 10723.3677 11965.7645 8723.9772 7251.3192 -0.2687 Not Balanced, >0.1 0.3672 Not Balanced, >2 0.1094
age Contin. 41.8193 10.6919 40.9727 10.3332 -0.0814 Balanced, <0.1 0.9340 Balanced, <2 0.0383
sex Binary 0.6598 . 0.6370 . -0.0228 Balanced, <0.1 . 0.0228
marry_dummy Binary 0.6354 . 0.6227 . -0.0127 Balanced, <0.1 . 0.0127
child_dummy Binary 0.3889 . 0.3971 . 0.0082 Balanced, <0.1 . 0.0082
inc Contin. 368.3451 258.2984 348.8679 268.7081 -0.0728 Balanced, <0.1 1.0822 Balanced, <2 0.0579
pmoney Contin. 3.5957 3.2636 3.5924 3.3758 -0.0010 Balanced, <0.1 1.0699 Balanced, <2 0.0456
area_kanto Binary 0.0855 . 0.0934 . 0.0079 Balanced, <0.1 . 0.0079
area_tokai Binary 0.1741 . 0.1144 . -0.0597 Balanced, <0.1 . 0.0597
area_keihanshin Binary 0.1936 . 0.1951 . 0.0015 Balanced, <0.1 . 0.0015
job_dummy1 Binary 0.6039 . 0.5608 . -0.0431 Balanced, <0.1 . 0.0431
job_dummy2 Binary 0.0550 . 0.0629 . 0.0079 Balanced, <0.1 . 0.0079
job_dummy3 Binary 0.0674 . 0.0686 . 0.0013 Balanced, <0.1 . 0.0013
job_dummy4 Binary 0.0107 . 0.0119 . 0.0012 Balanced, <0.1 . 0.0012
job_dummy5 Binary 0.0959 . 0.1147 . 0.0188 Balanced, <0.1 . 0.0188
job_dummy6 Binary 0.1012 . 0.1026 . 0.0014 Balanced, <0.1 . 0.0014
job_dummy7 Binary 0.0372 . 0.0481 . 0.0109 Balanced, <0.1 . 0.0109
fam_str_dummy1 Binary 0.1372 . 0.1606 . 0.0234 Balanced, <0.1 . 0.0234
fam_str_dummy2 Binary 0.1574 . 0.1513 . -0.0060 Balanced, <0.1 . 0.0060
fam_str_dummy3 Binary 0.6268 . 0.5915 . -0.0354 Balanced, <0.1 . 0.0354
fam_str_dummy4 Binary 0.0640 . 0.0656 . 0.0016 Balanced, <0.1 . 0.0016
Balance tally for mean differences
count
Balanced, <0.1 20
Not Balanced, >0.1 1
Variable with the greatest mean difference
Variable Diff.Adj M.Threshold
TVwatch_day -0.2687 Not Balanced, >0.1
Balance tally for variance ratios
count
Balanced, <2 4
Not Balanced, >2 1
Variable with the greatest variance ratio
Variable V.Ratio.Adj V.Threshold
TVwatch_day 0.3672 Not Balanced, >2
Effective sample sizes
Control Treated
Unadjusted 5856. 4144.
Adjusted 1487.52 2626.6
cobaltパッケージはWeightItのオブジェクトにも対応しているのでbal.tab()やlove.plot()でバランスを確認することができます。bal_tab_obj()関数はマッチングの節で定義したものを流用しています。この例ではTVwatch_dayのバランスが悪いことがわかります。
推定
推定値はマッチングのときと同じような方法で計算することにします。分散の均一性は仮定できませんがマッチングと異なり誤差がクラスタ構造にはなっていないので頑健標準誤差を利用します。頑健標準誤差はsandwitchパッケージのvcovHC()関数で利用することができます。共変量による調整を再度行わない場合は次のようになります。
fit1 <- lm(gamesecond ~ cm_dummy, df_ds3, weights = W.out$weights) coeftest(fit1, vcov. = vcovHC) coefci(fit1, vcov. = vcovHC)
t test of coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2639.41 226.01 11.6785 < 2e-16 ***
cm_dummy 1503.92 750.62 2.0036 0.04514 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
2.5 % 97.5 % (Intercept) 2196.39443 3082.430 cm_dummy 32.54389 2975.293
共変量による調整を再度行う場合は次のようになります。
wd_cen <- df_ds3 wd_cen[cov_names] <- scale(wd_cen[cov_names], scale = FALSE) fit2 <- glm(formula(str_c("gamesecond ~ cm_dummy * (", str_c(cov_names, collapse = "+"), ")")), data = wd_cen, weights = W.out$weights) coeftest(fit2, vcov. = vcovHC)[1:2,] coefci(fit2, vcov. = vcovHC)[1:2,]
Estimate Std. Error z value Pr(>|z|) (Intercept) 2888.4946 234.9653 12.293280 9.842997e-35 cm_dummy 492.8469 407.7861 1.208592 2.268198e-01
2.5 % 97.5 % (Intercept) 2427.9710 3349.018 cm_dummy -306.3992 1292.093
因果効果の推定
ここから推定結果を得る一連の流れを説明します。基本的にはマッチングと同じです。まず重み付けと推定を行い複数の推定結果を得ます。共変量のバランスと推定値の関係からモデル依存性が低下しているかを確認し、モデル依存性が低下している推定結果に基づいて結果の解釈を行います。
重み付け
マッチングのときと同じく重み付けでもどのような手法やモデルを使うと適切なバランシングができるかわからないので複数の手法やモデルを使って推定を行います。
傾向スコアの算出には、ロジスティック回帰、Covariate Balancing Propensity Score(CBPS)、Generalized Boosted Models(GBM)を使います。ロジスティック回帰とGBMはマッチングのガイダンス(Stuart, 2010)で傾向スコア算出時に利用を推奨されている手法でもあり、よく使われます。CBPSも近年よく使われる手法でこちらのチュートリアルでは利用が推奨されています。CBPSについては下記の記事も参考になるかもしれません。
CBPSでは使うモーメント条件によって過剰識別と丁度識別の2種類がありますが両方を使います。過剰識別と丁度識別を使い分けるために、method名を過剰識別は"cbps"、丁度識別は"cbpsexact"としています。
モデルは、処置の予測よりも共変量のバランス改善を意図したものになっています。そのため、バランスが悪い共変量の2乗や対数変換、交互作用を入れたモデルになっています。モデルの一部はマッチングで利用したものを流用しています。GBMは非線形モデルなので交互作用などを入れたformulaは除外しても問題ありません。
# methodの設定 method_settings <- c("ps", "cbps", "cbpsexact", "gbm") # モデルの設定 formula_settings <- c( str_c("cm_dummy ~ ", lt_base_str), str_c("cm_dummy ~ ", lt_str), str_c("cm_dummy ~ I(TVwatch_day^2) + ", lt_str), str_c("cm_dummy ~ I(TVwatch_day^2) + log(TVwatch_day) + ", lt_str), str_c("cm_dummy ~ I(TVwatch_day^2) + log(TVwatch_day) + TVwatch_day * log(TVwatch_day) + ", lt_str), str_c("cm_dummy ~ I(TVwatch_day^2) + log(TVwatch_day) + I(log(TVwatch_day)^2) + TVwatch_day * log(TVwatch_day) + ", lt_str), str_c("cm_dummy ~ I(TVwatch_day^2) + I(age^2) + I(inc^2) + I(pmoney^2) + ", lt_str), str_c("cm_dummy ~ I(TVwatch_day^2) + log(TVwatch_day) + TVwatch_day * (age + inc + pmoney) + ", lt_str), str_c("cm_dummy ~ I(TVwatch_day^2) + log(TVwatch_day) + TVwatch_day * (area_kanto + area_tokai + area_keihanshin) + ", lt_str) ) %>% map(formula) names(formula_settings) <- str_c("f", str_pad(1:length(formula_settings), 2, pad = 0)) # 重み付け実行の関数 exec_weighting <- function(dat, method_settings, formula_settings, estimand = "ATE", n_worker = 8) { # furrrの設定 plan(multisession, workers = n_worker) # 設定の組み合わせ crossing(method = method_settings, formula = formula_settings) %>% bind_cols( # 設定名 crossing( method = method_settings, formula = names(formula_settings) ) %>% mutate(name = str_c(method, formula, sep = "_")) %>% dplyr::select(name) ) %>% mutate(wt_obj = future_pmap(list(method, formula), function(method, formula) { if (method != "cbpsexact") { weightit( formula = formula, data = dat, estimand = estimand, method = method ) } else { # 丁度識別のCBPS weightit( formula = formula, data = dat, estimand = estimand, method = "cbps", over = FALSE ) } }, .options = furrr_options(seed = TRUE) ) ) %>% mutate(wt_smmry = map(wt_obj, ~ summary(.))) %>% mutate(cblt_smmry = map(wt_obj, ~ bal_tab_obj(.))) } # 重み付けの実行 df_wbal <- exec_weighting(df_ds3, method_settings, formula_settings)
重み付けでも一部のバランス指標を抽出します。ここではSMDの最大値と平均値、KS統計量の最大値と平均値、SMDが0.1を上回った共変量の数、重みサマリの各指標を抽出します。
# バランス指標抽出関数 summary_weighting_balance <- function(dat) { dat %>% mutate(cblt_tbl = map(cblt_smmry, ~ .$Balance)) %>% mutate( max_smd = map(cblt_tbl, ~ tibble(max_smd = max(abs(.$Diff.Adj)))), mean_smd = map(cblt_tbl, ~ tibble(mean_smd = mean(abs(.$Diff.Adj)))), max_ks = map(cblt_tbl, ~ tibble(max_ks = max(.$KS.Adj))), mean_ks = map(cblt_tbl, ~ tibble(mean_ks = mean(.$KS.Adj))), n_unbalance = map(cblt_tbl, ~ tibble(n_unbalance = sum(abs(.$Diff.Adj) >= 0.1))), max_weight_tr = map(wt_smmry, ~ tibble(max_weight_tr = max(.$weight.range$treated))), max_weight_ctl = map(wt_smmry, ~ tibble(max_weight_ctl = max(.$weight.range$control))), coef.of.var_tr = map(wt_smmry, ~ tibble(coef.of.var_tr = .$coef.of.var["treated"])), coef.of.var_ctl = map(wt_smmry, ~ tibble(coef.of.var_ctl = .$coef.of.var["control"])), coef.of.var_all = map(wt_smmry, ~ tibble(coef.of.var_all = .$coef.of.var["overall"])), scaled.mad_tr = map(wt_smmry, ~ tibble(scaled.mad_tr = .$scaled.mad["treated"])), scaled.mad_ctl = map(wt_smmry, ~ tibble(scaled.mad_ctl = .$scaled.mad["control"])), scaled.mad_all = map(wt_smmry, ~ tibble(scaled.mad_all = .$scaled.mad["overall"])), negative.entropy_tr = map(wt_smmry, ~ tibble(negative.entropy_tr = .$negative.entropy["treated"])), negative.entropy_ctl = map(wt_smmry, ~ tibble(negative.entropy_ctl = .$negative.entropy["control"])), negative.entropy_all = map(wt_smmry, ~ tibble(negative.entropy_all = .$negative.entropy["overall"])), num.zeros_tr = map(wt_smmry, ~ tibble(num.zeros_tr = .$num.zeros["treated"])), num.zeros_ctl = map(wt_smmry, ~ tibble(num.zeros_ctl = .$num.zeros["control"])), num.zeros_all = map(wt_smmry, ~ tibble(num.zeros_all = .$num.zeros["overall"])) ) %>% dplyr::select(-(method:formula), -(wt_obj:cblt_tbl)) %>% unnest(max_smd) %>% unnest(mean_smd) %>% unnest(max_ks) %>% unnest(mean_ks) %>% unnest(n_unbalance) %>% unnest(max_weight_tr) %>% unnest(max_weight_ctl) %>% unnest(coef.of.var_tr) %>% unnest(coef.of.var_ctl) %>% unnest(coef.of.var_all) %>% unnest(scaled.mad_tr) %>% unnest(scaled.mad_ctl) %>% unnest(scaled.mad_all) %>% unnest(negative.entropy_tr) %>% unnest(negative.entropy_ctl) %>% unnest(negative.entropy_all) %>% unnest(num.zeros_tr) %>% unnest(num.zeros_ctl) %>% unnest(num.zeros_all) } df_wbal_summary <- summary_weighting_balance(df_wbal) df_wbal_summary %>% filter(max_smd <= 0.1) %>% kable()
| name | max_smd | mean_smd | max_ks | mean_ks | n_unbalance | max_weight_tr | max_weight_ctl | coef.of.var_tr | coef.of.var_ctl | coef.of.var_all | scaled.mad_tr | scaled.mad_ctl | scaled.mad_all | negative.entropy_tr | negative.entropy_ctl | negative.entropy_all | num.zeros_tr | num.zeros_ctl | num.zeros_all |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cbpsexact_f01 | 0.0288006 | 0.0018343 | 0.1548866 | 0.01590812 | 0 | 14.54744 | 38.202066 | 0.7692866 | 0.9511370 | 0.8792651 | 0.4696642 | 0.3595379 | 0.4416589 | 1.088429 | 0.7237768 | 0.9059490 | 0 | 0 | 0 |
| cbpsexact_f02 | 0.0258162 | 0.0013977 | 0.1583956 | 0.01181424 | 0 | 16.00349 | 37.161665 | 0.7995245 | 0.9676852 | 0.9027967 | 0.4780169 | 0.3654019 | 0.4472194 | 1.097967 | 0.7282825 | 0.9128483 | 0 | 0 | 0 |
| cbpsexact_f04 | 0.0828692 | 0.0033746 | 0.08364243 | 0.01070845 | 0 | 31.03608 | 16.959674 | 0.9685923 | 0.7219435 | 0.9036802 | 0.5691839 | 0.4236407 | 0.5104917 | 1.182382 | 0.7223476 | 0.9519313 | 0 | 0 | 0 |
| cbpsexact_f05 | 0.0922689 | 0.0036482 | 0.0826121 | 0.009991484 | 0 | 35.05201 | 14.706056 | 0.9966402 | 0.6958145 | 0.9137526 | 0.5828990 | 0.4334729 | 0.5203029 | 1.194600 | 0.7216022 | 0.9578759 | 0 | 0 | 0 |
| cbpsexact_f06 | 0.0878660 | 0.0034205 | 0.08579514 | 0.00999003 | 0 | 37.16435 | 15.446625 | 1.0214410 | 0.6993982 | 0.9310223 | 0.5823365 | 0.4303702 | 0.5170263 | 1.198174 | 0.7199601 | 0.9587561 | 0 | 0 | 0 |
| cbpsexact_f07 | 0.0881439 | 0.0031368 | 0.09930372 | 0.01229953 | 0 | 24.11497 | 19.473053 | 0.9481542 | 0.7508862 | 0.9016856 | 0.5620010 | 0.4230243 | 0.5123772 | 1.177623 | 0.7280766 | 0.9528211 | 0 | 0 | 0 |
| cbpsexact_f09 | 0.0763735 | 0.0035709 | 0.07372083 | 0.01154189 | 0 | 43.03984 | 16.120321 | 1.0960893 | 0.7109629 | 0.9854306 | 0.5668671 | 0.4075788 | 0.5010488 | 1.208547 | 0.7125242 | 0.9606105 | 0 | 0 | 0 |
| ps_f03 | 0.0846127 | 0.0197240 | 0.08740647 | 0.02207004 | 0 | 23.73619 | 13.388417 | 0.8291170 | 0.6238368 | 0.7753651 | 0.4870419 | 0.3631170 | 0.4454298 | 1.063878 | 0.6547901 | 0.8569223 | 0 | 0 | 0 |
| ps_f04 | 0.0830148 | 0.0215155 | 0.05915604 | 0.02407283 | 0 | 29.51638 | 10.967334 | 0.9373788 | 0.5749447 | 0.8382406 | 0.5162862 | 0.3621399 | 0.4532817 | 1.121922 | 0.6357876 | 0.8791386 | 0 | 0 | 0 |
| ps_f05 | 0.0890843 | 0.0231113 | 0.07493468 | 0.02233309 | 0 | 33.29723 | 9.329877 | 0.9174523 | 0.5626715 | 0.8172570 | 0.5135187 | 0.3683285 | 0.4531960 | 1.098163 | 0.6355538 | 0.8657633 | 0 | 0 | 0 |
| ps_f06 | 0.0736185 | 0.0234370 | 0.06218606 | 0.02340029 | 0 | 41.07460 | 10.333581 | 1.0153816 | 0.5702867 | 0.8897413 | 0.5226541 | 0.3674931 | 0.4545276 | 1.132393 | 0.6354166 | 0.8840389 | 0 | 0 | 0 |
| ps_f07 | 0.0968228 | 0.0214850 | 0.08841285 | 0.02285202 | 0 | 20.66597 | 13.422394 | 0.8241267 | 0.6042638 | 0.7676257 | 0.4913547 | 0.3586025 | 0.4462315 | 1.067775 | 0.6426314 | 0.8535742 | 0 | 0 | 0 |
| ps_f08 | 0.0915374 | 0.0243690 | 0.065773 | 0.0232067 | 0 | 19.47717 | 17.506944 | 0.8777150 | 0.6191597 | 0.8097200 | 0.5124174 | 0.3636894 | 0.4512132 | 1.099274 | 0.6408396 | 0.8693585 | 0 | 0 | 0 |
| ps_f09 | 0.0986627 | 0.0226648 | 0.0635386 | 0.02503109 | 0 | 36.71914 | 11.685330 | 1.0332330 | 0.5850105 | 0.9126481 | 0.5279739 | 0.3551915 | 0.4571176 | 1.161142 | 0.6324927 | 0.8992717 | 0 | 0 | 0 |
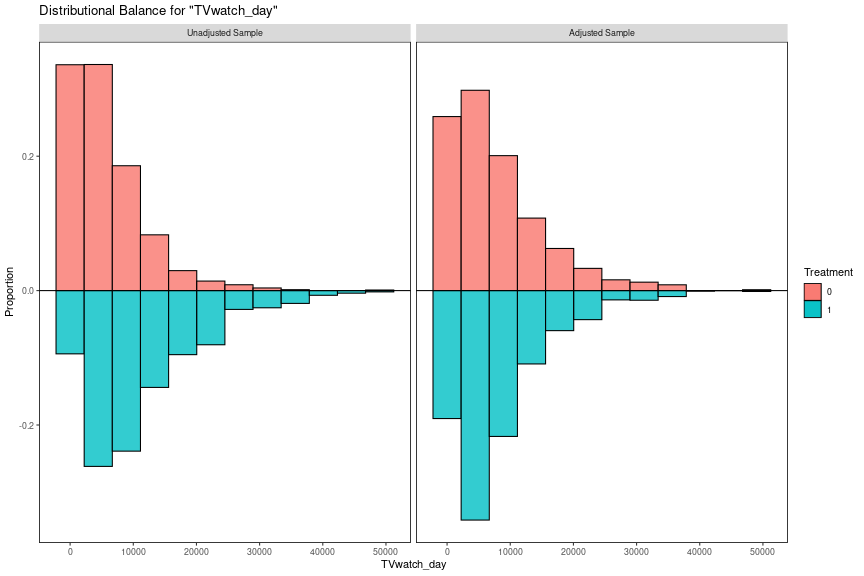
SMDの最大値が0.1以下になった結果を見ると、"cbpsexact_f01"と"cbpsexact_f02"のSMDは他のケースと比較して小さく、一見バランスがよさそうに見えます。しかし、KS統計量の最大値が他と比較して大きく、分布の差が大きいことがわかります。このようなケースは分布に異常が見られることが多いので確認する必要があります。ここでは"cbpsexact_f01"でKS統計量が一番大きかったTVwatch_dayについて分布を確認します。bal_plot_hist()関数はマッチングの節で定義したものを使います。
wt_obj <- df_wbal %>% filter(name == "cbpsexact_f01") %>% pull(wt_obj) %>% .[[1]] bal_plot_hist(wt_obj, "TVwatch_day")
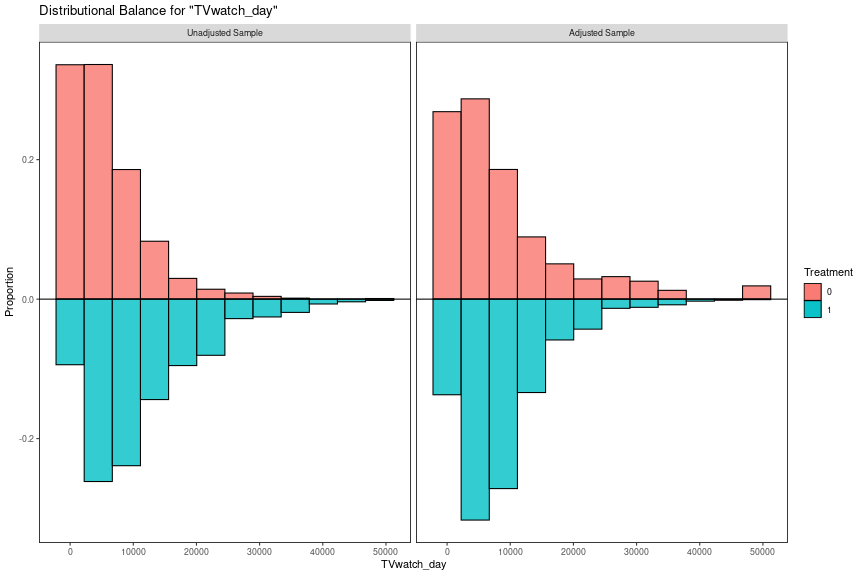
SMDは小さいのですが、重み付け後の分布はバランスが悪いことがわかります。特に対照群の分布はTVwatch_dayが小さいときの頻度は高いままで、それと釣り合うようにTVwatch_dayが大きいときの頻度が不自然に低くなっていることが確認できます。このようなケースの推定値は信頼性が低いと考えてよいでしょう。
推定
次に、各ケースについてATEを推定し、結果を確認しやすいように推定値と標準偏差、信頼区間を抽出してまとめます。推定値などの抽出にはマッチングの節で定義したsummary_ate_estimation()関数を使います。
# ATE推定の関数 estimate_ate_after_weighting <- function(df_bal, dat, outcome_name, treat_name, covnames) { lm_w <- function(obj, f, dat) { lm(f, data = dat %>% mutate(weights = obj$weights), weights = weights) } coeftest_tidy <- function(fit, tr_name) { coeftest(fit, vcov. = vcovHC) %>% tidy() %>% filter(term %in% c("(Intercept)", tr_name)) %>% mutate(term = c("E0", "ATE")) } coefci_tidy <- function(fit, tr_name) { d <- coefci(fit, vcov. = vcovHC) %>% data.frame() d <- d[rownames(d) %in% c("(Intercept)", tr_name),] colnames(d) <- c("ci2.5", "ci97.5") d %>% mutate(ci_name = c("E0", "ATE")) } centered_covnames <- covnames formula_wo <- formula(str_c(outcome_name, "~", treat_name)) formula_w <- formula(str_c(outcome_name, "~", treat_name, " * (", str_c(centered_covnames, collapse = "+"), ")")) wd_cen <- dat wd_cen[centered_covnames] <- scale(wd_cen[centered_covnames], scale = FALSE) df_bal %>% mutate(fit_wo_ca = map(.x = wt_obj, .f = lm_w, f = formula_wo, dat = dat)) %>% mutate(ate_est_wo_ca = map(.x = fit_wo_ca, .f = coeftest_tidy, tr_name = treat_name)) %>% mutate(ate_ci_wo_ca = map(.x = fit_wo_ca, .f = coefci_tidy, tr_name = treat_name)) %>% mutate(fit_w_ca = map(.x = wt_obj, .f = lm_w, f = formula_w, dat = wd_cen)) %>% mutate(ate_est_w_ca = map(.x = fit_w_ca, .f = coeftest_tidy, tr_name = treat_name)) %>% mutate(ate_ci_w_ca = map(.x = fit_w_ca, .f = coefci_tidy, tr_name = treat_name)) } # ATE推定 df_wbal <- estimate_ate_after_weighting(df_wbal, df_ds3, "gamesecond", "cm_dummy", cov_names2) # 推定値と標準偏差、信頼区間を抽出 df_wbal_est_summary <- summary_ate_estimation(df_wbal, df_wbal_summary) df_wbal_est_summary %>% filter(max_smd <= 0.1) %>% kable()
| name | estimate_wo | std.error_wo | p.value_wo | ci2.5_wo | ci97.5_wo | estimate_w | std.error_w | p.value_w | ci2.5_w | ci97.5_w | abs_diff_est | max_smd | mean_smd | max_ks | mean_ks | n_unbalance | max_weight_tr | max_weight_ctl | coef.of.var_tr | coef.of.var_ctl | coef.of.var_all | scaled.mad_tr | scaled.mad_ctl | scaled.mad_all | negative.entropy_tr | negative.entropy_ctl | negative.entropy_all | num.zeros_tr | num.zeros_ctl | num.zeros_all |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cbpsexact_f01 | 452.3585 | 517.1870 | 0.3817844 | -561.4321 | 1466.149 | 270.7817 | 388.7290 | 0.4860806 | -491.2059 | 1032.769 | 181.576799 | 0.0288006 | 0.0018343 | 0.1548866 | 0.0159081 | 0 | 14.54744 | 38.202066 | 0.7692866 | 0.9511370 | 0.8792651 | 0.4696642 | 0.3595379 | 0.4416589 | 1.088429 | 0.7237768 | 0.9059490 | 0 | 0 | 0 |
| cbpsexact_f02 | 223.1354 | 469.8551 | 0.6348668 | -697.8753 | 1144.146 | 246.4129 | 391.1446 | 0.5287227 | -520.3096 | 1013.135 | 23.277521 | 0.0258162 | 0.0013977 | 0.1583956 | 0.0118142 | 0 | 16.00349 | 37.161665 | 0.7995245 | 0.9676852 | 0.9027967 | 0.4780169 | 0.3654019 | 0.4472194 | 1.097967 | 0.7282825 | 0.9128483 | 0 | 0 | 0 |
| cbpsexact_f04 | 483.2522 | 491.4499 | 0.3254741 | -480.0886 | 1446.593 | 516.2167 | 406.9739 | 0.2046752 | -281.5346 | 1313.968 | 32.964548 | 0.0828692 | 0.0033746 | 0.0836424 | 0.0107084 | 0 | 31.03608 | 16.959674 | 0.9685923 | 0.7219435 | 0.9036802 | 0.5691839 | 0.4236407 | 0.5104917 | 1.182382 | 0.7223476 | 0.9519313 | 0 | 0 | 0 |
| cbpsexact_f05 | 519.3537 | 484.3620 | 0.2836368 | -430.0933 | 1468.801 | 554.4055 | 416.6512 | 0.1833437 | -262.3152 | 1371.126 | 35.051748 | 0.0922689 | 0.0036482 | 0.0826121 | 0.0099915 | 0 | 35.05201 | 14.706056 | 0.9966402 | 0.6958145 | 0.9137526 | 0.5828990 | 0.4334729 | 0.5203029 | 1.194600 | 0.7216022 | 0.9578759 | 0 | 0 | 0 |
| cbpsexact_f06 | 515.9220 | 483.2473 | 0.2857200 | -431.3400 | 1463.184 | 554.6215 | 420.9617 | 0.1876980 | -270.5488 | 1379.792 | 38.699476 | 0.0878660 | 0.0034205 | 0.0857951 | 0.0099900 | 0 | 37.16435 | 15.446625 | 1.0214410 | 0.6993982 | 0.9310223 | 0.5823365 | 0.4303702 | 0.5170263 | 1.198174 | 0.7199601 | 0.9587561 | 0 | 0 | 0 |
| cbpsexact_f07 | 387.0106 | 475.5424 | 0.4157618 | -545.1482 | 1319.169 | 380.9944 | 393.5961 | 0.3330762 | -390.5336 | 1152.522 | 6.016191 | 0.0881439 | 0.0031368 | 0.0993037 | 0.0122995 | 0 | 24.11497 | 19.473053 | 0.9481542 | 0.7508862 | 0.9016856 | 0.5620010 | 0.4230243 | 0.5123772 | 1.177623 | 0.7280766 | 0.9528211 | 0 | 0 | 0 |
| cbpsexact_f09 | 626.0625 | 521.3668 | 0.2298533 | -395.9213 | 1648.046 | 610.9804 | 397.3024 | 0.1241239 | -167.8127 | 1389.774 | 15.082019 | 0.0763735 | 0.0035709 | 0.0737208 | 0.0115419 | 0 | 43.03984 | 16.120321 | 1.0960893 | 0.7109629 | 0.9854306 | 0.5668671 | 0.4075788 | 0.5010488 | 1.208547 | 0.7125242 | 0.9606105 | 0 | 0 | 0 |
| ps_f03 | 660.1466 | 566.4881 | 0.2439125 | -450.2841 | 1770.577 | 416.6336 | 402.3724 | 0.3004873 | -372.0978 | 1205.365 | 243.512924 | 0.0846127 | 0.0197240 | 0.0874065 | 0.0220700 | 0 | 23.73619 | 13.388417 | 0.8291170 | 0.6238368 | 0.7753651 | 0.4870419 | 0.3631170 | 0.4454298 | 1.063878 | 0.6547901 | 0.8569223 | 0 | 0 | 0 |
| ps_f04 | 565.0875 | 519.9527 | 0.2771490 | -454.1246 | 1584.299 | 429.5039 | 406.0259 | 0.2901614 | -366.3890 | 1225.397 | 135.583510 | 0.0830148 | 0.0215155 | 0.0591560 | 0.0240728 | 0 | 29.51638 | 10.967334 | 0.9373788 | 0.5749447 | 0.8382406 | 0.5162862 | 0.3621399 | 0.4532817 | 1.121922 | 0.6357876 | 0.8791386 | 0 | 0 | 0 |
| ps_f05 | 549.6309 | 509.6091 | 0.2808214 | -449.3055 | 1548.567 | 441.8253 | 410.9804 | 0.2823775 | -363.7794 | 1247.430 | 107.805560 | 0.0890843 | 0.0231113 | 0.0749347 | 0.0223331 | 0 | 33.29723 | 9.329877 | 0.9174523 | 0.5626715 | 0.8172570 | 0.5135187 | 0.3683285 | 0.4531960 | 1.098163 | 0.6355538 | 0.8657633 | 0 | 0 | 0 |
| ps_f06 | 604.1180 | 519.7999 | 0.2451769 | -414.7944 | 1623.030 | 451.9053 | 418.1885 | 0.2798898 | -367.8289 | 1271.639 | 152.212702 | 0.0736185 | 0.0234370 | 0.0621861 | 0.0234003 | 0 | 41.07460 | 10.333581 | 1.0153816 | 0.5702867 | 0.8897413 | 0.5226541 | 0.3674931 | 0.4545276 | 1.132393 | 0.6354166 | 0.8840389 | 0 | 0 | 0 |
| ps_f07 | 429.3587 | 511.4784 | 0.4012389 | -573.2419 | 1431.959 | 312.9999 | 396.3901 | 0.4297651 | -464.0050 | 1090.005 | 116.358843 | 0.0968228 | 0.0214850 | 0.0884129 | 0.0228520 | 0 | 20.66597 | 13.422394 | 0.8241267 | 0.6042638 | 0.7676257 | 0.4913547 | 0.3586025 | 0.4462315 | 1.067775 | 0.6426314 | 0.8535742 | 0 | 0 | 0 |
| ps_f08 | 694.2335 | 532.4269 | 0.1922964 | -349.4304 | 1737.897 | 526.0302 | 410.5195 | 0.2000912 | -278.6712 | 1330.732 | 168.203291 | 0.0915374 | 0.0243690 | 0.0657730 | 0.0232067 | 0 | 19.47717 | 17.506944 | 0.8777150 | 0.6191597 | 0.8097200 | 0.5124174 | 0.3636894 | 0.4512132 | 1.099274 | 0.6408396 | 0.8693585 | 0 | 0 | 0 |
| ps_f09 | 804.0417 | 564.2123 | 0.1541684 | -301.9280 | 1910.012 | 526.5598 | 398.6619 | 0.1865924 | -254.8982 | 1308.018 | 277.481969 | 0.0986627 | 0.0226648 | 0.0635386 | 0.0250311 | 0 | 36.71914 | 11.685330 | 1.0332330 | 0.5850105 | 0.9126481 | 0.5279739 | 0.3551915 | 0.4571176 | 1.161142 | 0.6324927 | 0.8992717 | 0 | 0 | 0 |
SMDの最大値が0.1以下のケースについて信頼区間を確認すると、再調整の有無にかかわらず信頼区間に0が含まれていることがわかります。マッチングと同様に、統計的に有意な効果は得られなかったということになります。重み付けでも、SMDが基準を満たしていても推定値にばらつきがあるので、どのぐらいの推定値が妥当なのかを検討していきます。
結果の検証
まず、共変量による再調整がないときについて、SMDの最大値と推定値の関係を見てみましょう。
df_wbal_est_summary_ <- df_wbal_est_summary %>% bind_cols(df_wbal %>% dplyr::select(method)) df_wbal_est_summary_ %>% ggplot(aes(x = max_smd, y = estimate_wo, group = method, color = method)) + geom_point()
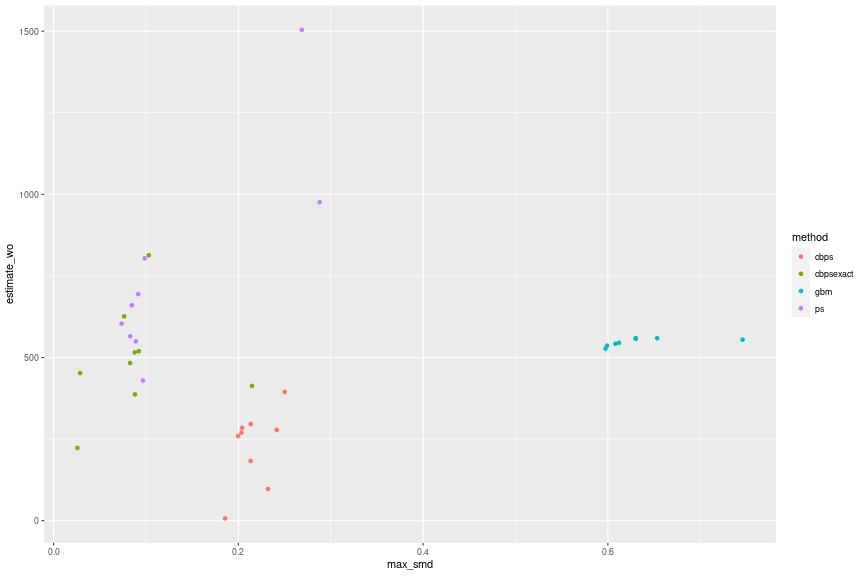
手法によって傾向が大きく異なることがわかります。GBMと過剰識別のCBPSではSMDが0.1以下になる結果を得られていません。ロジスティック回帰と丁度識別のCBPSではモデルによって傾向が異なりますが、SMDが0.1を下回ったあたりから徐々に推定値のばらつきが小さくなりモデル依存性が弱くなっているようにも見えます。SMDが0.1を下回ったあたりでは400から800、SMDが0.09を下回ったあたりでは400から650、SMDが0.085を下回ったあたりでは500から650に推定値が収まっています。なお、丁度識別のCBPSでSMDが非常に小さい2つのケースについては前述の通り共変量の分布が歪んでいるので基本的には無視しています。
次に、共変量による再調整があるときについて、SMDの最大値と推定値の関係を見てみましょう。
df_wbal_est_summary_ %>% ggplot(aes(x = max_smd, y = estimate_w, group = method, color = method)) + geom_point()
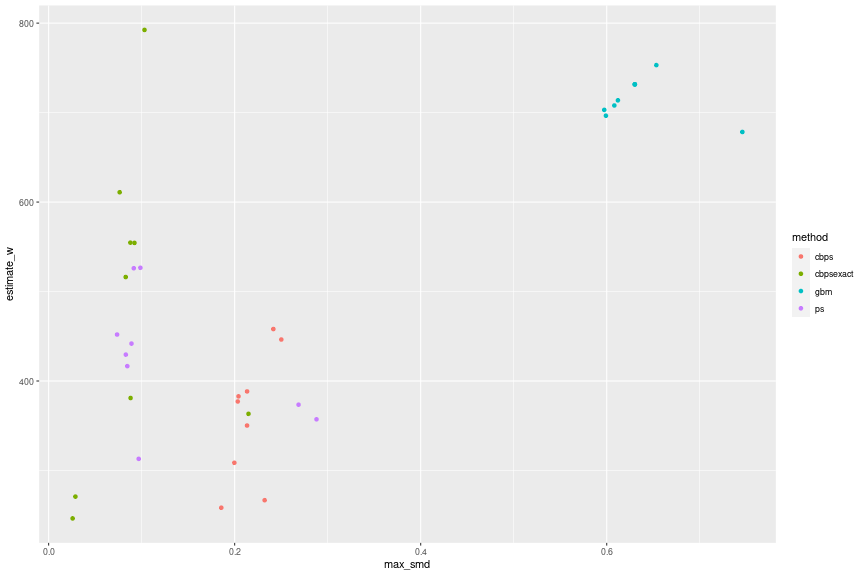
共変量による再調整の影響は手法によって異なるようで、ロジスティック回帰では推定値が小さくなり、過剰識別のCBPSとGBMでは推定値が大きくなり、丁度識別のCBPSではほぼ変わらないことがわかります。SMDが0.1を下回ったあたりでは推定値は400から600程度になっています。信頼区間も表示すると次のようになります。
df_wbal_est_summary_ %>% ggplot(aes(x = max_smd, y = estimate_w, group = method, color = method)) + geom_errorbar(aes(ymax = ci97.5_w, ymin = ci2.5_w)) + geom_point()
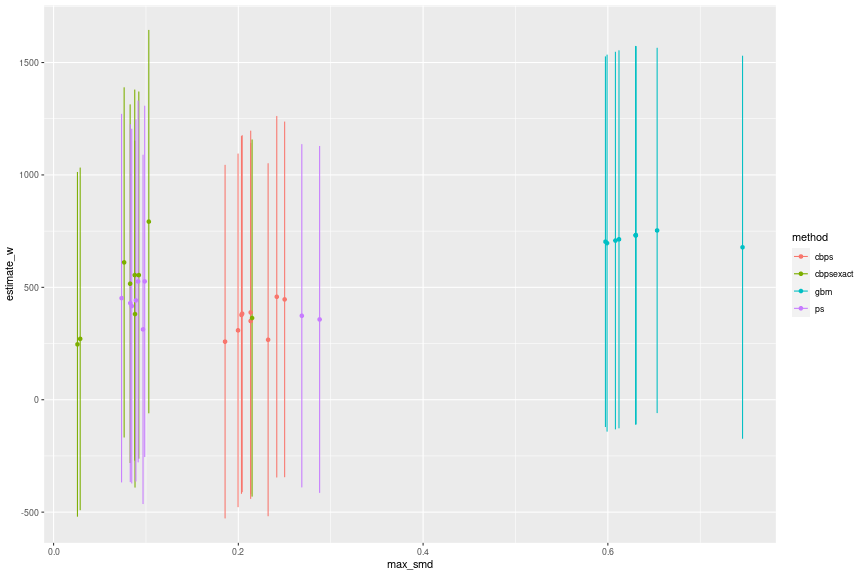
推定値のみを見ると結果のばらつきが大きく、どの結果を採用すべきか迷いますが、信頼区間も表示すると誤差の範囲内でのばらつきであることが実感できると思います。SMDの最大値が0.03から0.1の結果のみを表示すると以下のようになります。
df_wbal_est_summary_ %>% filter(max_smd <= 0.1, max_smd >= 0.03) %>% ggplot(aes(x = max_smd, y = estimate_w, group = method, color = method)) + geom_errorbar(aes(ymax = ci97.5_w, ymin = ci2.5_w)) + geom_point()
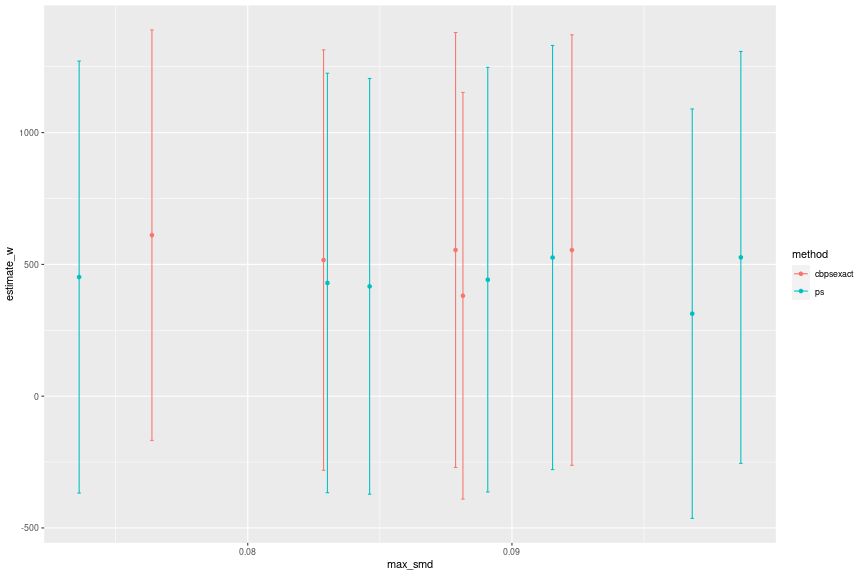
推定値は500前後であることがわかると思います。
重み付けによる結果を一つだけ報告するならば、KS統計量や重み指標に異常がなく、SMDが最小の"ps_f06"がよさそうです。共変量による再調整があったときの推定値は452で、信頼区間は-367.8289から1271.639です。
念のため"ps_f06"の共変量のバランスも確認しておきましょう。
df_wbal %>% filter(name == "ps_f06") %>% pull(cblt_smmry)
[[1]]
Call
weightit(formula = formula, data = df_ds3, method = method, estimand = "ATE",
stop.method = "es.mean")
Balance Measures
Type M.0.Adj SD.0.Adj M.1.Adj SD.1.Adj Diff.Adj M.Threshold V.Ratio.Adj V.Threshold KS.Adj
prop.score Distance 0.4045 0.2501 0.4209 0.2562 0.0736 Balanced, <0.1 1.0492 Balanced, <2 0.0622
I(TVwatch_day^2) Contin. 114489789.5583 222256258.6291 128458018.0100 245022853.7194 0.0567 Balanced, <0.1 1.2154 Balanced, <2 0.0526
log(TVwatch_day) Contin. 8.3962 1.2934 8.4524 1.2988 0.0471 Balanced, <0.1 1.0083 Balanced, <2 0.0526
I(log(TVwatch_day)^2) Contin. 72.1694 19.9234 73.1283 20.2172 0.0519 Balanced, <0.1 1.0297 Balanced, <2 0.0526
TVwatch_day Contin. 7785.0691 7341.3000 8278.1696 7743.3397 0.0663 Balanced, <0.1 1.1125 Balanced, <2 0.0526
age Contin. 41.0498 10.7599 41.3001 10.3469 0.0241 Balanced, <0.1 0.9247 Balanced, <2 0.0292
sex Binary 0.6573 . 0.6350 . -0.0223 Balanced, <0.1 . 0.0223
marry_dummy Binary 0.6455 . 0.6215 . -0.0240 Balanced, <0.1 . 0.0240
child_dummy Binary 0.4080 . 0.3727 . -0.0353 Balanced, <0.1 . 0.0353
inc Contin. 363.1939 263.8307 344.7899 266.8328 -0.0688 Balanced, <0.1 1.0229 Balanced, <2 0.0513
pmoney Contin. 3.5383 3.3932 3.5776 3.4431 0.0116 Balanced, <0.1 1.0296 Balanced, <2 0.0461
area_kanto Binary 0.0889 . 0.0911 . 0.0023 Balanced, <0.1 . 0.0023
area_tokai Binary 0.1215 . 0.1050 . -0.0165 Balanced, <0.1 . 0.0165
area_keihanshin Binary 0.2111 . 0.1869 . -0.0242 Balanced, <0.1 . 0.0242
job_dummy1 Binary 0.5784 . 0.5473 . -0.0311 Balanced, <0.1 . 0.0311
job_dummy2 Binary 0.0610 . 0.0626 . 0.0016 Balanced, <0.1 . 0.0016
job_dummy3 Binary 0.0730 . 0.0687 . -0.0043 Balanced, <0.1 . 0.0043
job_dummy4 Binary 0.0123 . 0.0181 . 0.0058 Balanced, <0.1 . 0.0058
job_dummy5 Binary 0.1033 . 0.1266 . 0.0233 Balanced, <0.1 . 0.0233
job_dummy6 Binary 0.0979 . 0.0956 . -0.0023 Balanced, <0.1 . 0.0023
job_dummy7 Binary 0.0430 . 0.0469 . 0.0039 Balanced, <0.1 . 0.0039
fam_str_dummy1 Binary 0.1481 . 0.1595 . 0.0113 Balanced, <0.1 . 0.0113
fam_str_dummy2 Binary 0.1508 . 0.1665 . 0.0157 Balanced, <0.1 . 0.0157
fam_str_dummy3 Binary 0.6142 . 0.5757 . -0.0385 Balanced, <0.1 . 0.0385
fam_str_dummy4 Binary 0.0704 . 0.0756 . 0.0052 Balanced, <0.1 . 0.0052
T Binary 0.0125 . 0.0085 . -0.0040 Balanced, <0.1 . 0.0040
F1 Binary 0.1244 . 0.1112 . -0.0131 Balanced, <0.1 . 0.0131
F2 Binary 0.1566 . 0.1724 . 0.0158 Balanced, <0.1 . 0.0158
F3 Binary 0.0553 . 0.0760 . 0.0206 Balanced, <0.1 . 0.0206
M1 Binary 0.1448 . 0.1495 . 0.0047 Balanced, <0.1 . 0.0047
M2 Binary 0.3355 . 0.3274 . -0.0081 Balanced, <0.1 . 0.0081
M3 Binary 0.1708 . 0.1549 . -0.0159 Balanced, <0.1 . 0.0159
Balance tally for mean differences
count
Balanced, <0.1 32
Not Balanced, >0.1 0
Variable with the greatest mean difference
Variable Diff.Adj M.Threshold
inc -0.0688 Balanced, <0.1
Balance tally for variance ratios
count
Balanced, <2 8
Not Balanced, >2 0
Variable with the greatest variance ratio
Variable V.Ratio.Adj V.Threshold
I(TVwatch_day^2) 1.2154 Balanced, <2
Effective sample sizes
Control Treated
Unadjusted 5856. 4144.
Adjusted 4419.05 2040.62
KS統計量が大きいprop.score、TVwatch_day、incについては分布も確認しましょう。マッチングの節で定義したbal_plot_hist()関数を利用します。
wt_obj <- df_wbal %>% filter(name == "ps_f06") %>% pull(wt_obj) %>% .[[1]] bal_plot_hist(wt_obj, "prop.score") bal_plot_hist(wt_obj, "TVwatch_day") bal_plot_hist(wt_obj, "inc")
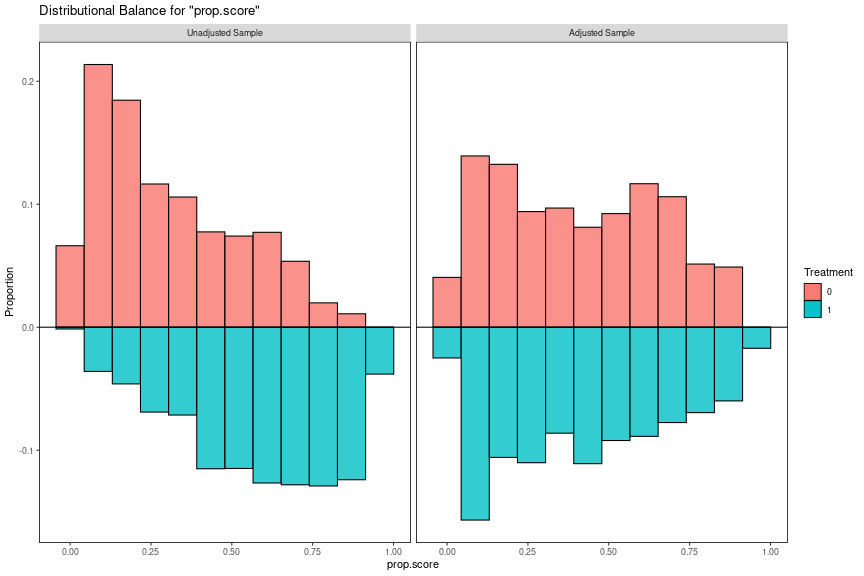
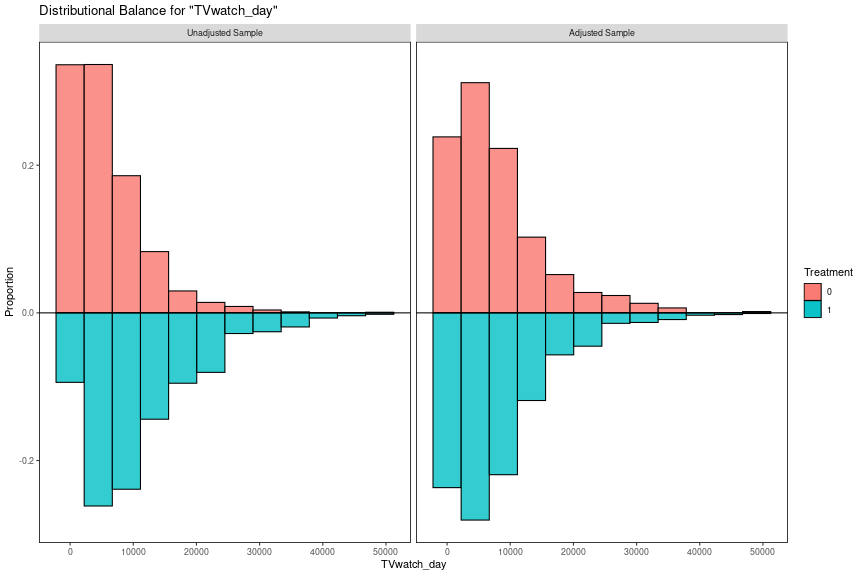
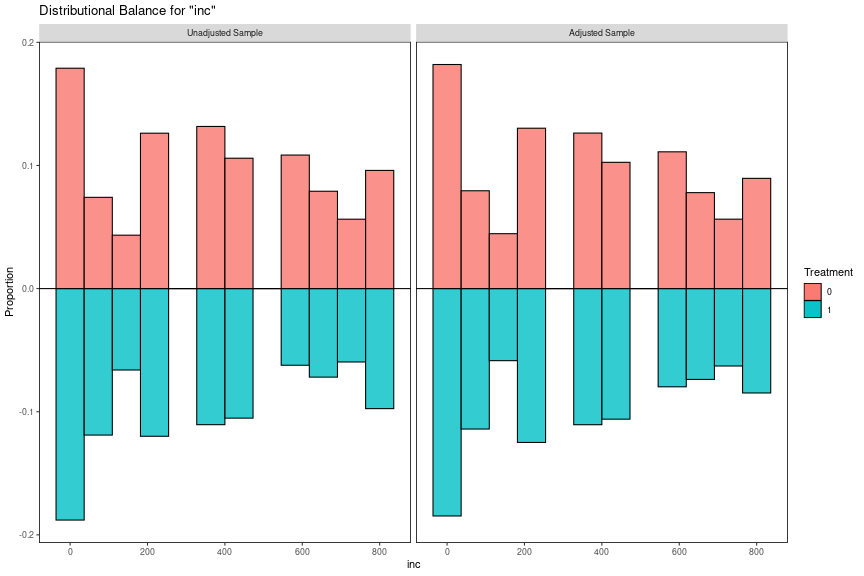
傾向スコアは重み付け後もバランスがやや悪いですが異常ではありません。マッチング前のデータを見ると処置群と対照群で傾向スコアの取りうる範囲も異なることがわかります。
この例ではマッチングと重み付けの推定値が異なっていますが、マッチングと重み付けでは推定している母集団や反事実への対処方法が異なるので推定値が異なることはよくあります(Kurth, 2006)。細かい違いはいろいろありますが、マッチングでは反事実のデータを類似サンプルに置き換えますが、重み付け法では結果変数の値に重みをつけるところが大きな違いで、特にレアケースの扱いに大きな差があります。マッチングではレアケースはペアになりにくかったり除外されたりしますが、重み付けでは大きな重みが付けられやすくなります。このことが理由で違いが生じている場合はマッチングでペアにならなかったサンプルを考慮したり、重み付けでcommon supportを設定したりすることで推定値の差を小さくできることがあります。
common supportを考慮したときの推定値を計算してみましょう。まず、処置群と対照群の傾向スコアの範囲を確認します。
formula_ps_f06 <- df_wbal %>% filter(name == "ps_f06") %>% pull(formula) %>% .[[1]] d <- tibble( ps = glm(formula_ps_f06, df_ds3, family = binomial)$fitted.values, tr = df_ds3$cm_dummy ) d_ <- d %>% group_by(tr) %>% summarise(max_ps = max(ps), min_ps = min(ps)) d_
# A tibble: 2 x 3
tr max_ps min_ps
<dbl> <dbl> <dbl>
1 0 0.903 0.00630
2 1 0.963 0.0243
処置群には傾向スコアが2.4%以下のサンプルはなく、対照群には90.3%以上のサンプルがありません。そこで、傾向スコアが2.4%から90.3%のサンプルのみを抽出して推定し直します。
ps <- d$ps min_ps <- max(d_$min_ps) max_ps <- min(d_$max_ps) cs_index <- which(ps >= min_ps & ps <= max_ps) W.out_cs <- weightit( formula_ps_f06, data = df_ds3[cs_index,], ps = ps[cs_index], estimand = "ATE") bal_tab_obj(W.out_cs) # 念のためバランスを確認 wd_cen <- df_ds3[cs_index,] wd_cen[cov_names2] <- scale(wd_cen[cov_names2], scale = FALSE) fit_cs <- glm(formula(str_c("gamesecond ~ cm_dummy * (", str_c(cov_names2, collapse = "+"), ")")), data = wd_cen, weights = W.out_cs$weights) coeftest(fit_cs, vcov. = vcovHC)[1:2,] coefci(fit_cs, vcov. = vcovHC)[1:2,]
Estimate Std. Error z value Pr(>|z|) (Intercept) 2956.5441 234.7656 12.5935996 2.28988e-36 cm_dummy 283.1162 421.2342 0.6721111 5.01513e-01
2.5 % 97.5 % (Intercept) 2496.4119 3416.676 cm_dummy -542.4877 1108.720
common supportを考慮することで推定値は小さくなりマッチングの結果に近づきました。common support外の実在しにくいサンプルを推定に使っていたことが、マッチングと重み付けで推定値が異なる原因の一つと考えられます。なお、上記の方法以外にも大きな重みの影響を除外することを目的とした方法として、閾値以上もしくは以下の重みを閾値に置き換えるweight trimmingが知られています。この方法は機械的に使用するとバイアスを増加させる可能性があることが指摘されているので利用する際は注意したほうがよいでしょう(Lee et al., 2011)。
ここで説明したもの以外にもマッチングと重み付けで推定値に差が生じる原因はあるので、推定値がほぼ一致するまで原因を調査するのは大変です。common supportは確認したほうがよいですが、全く正反対の結果が得られた場合など施策の採否に影響するケースを除けば大きな問題になることはないと思います。この例ではマッチングでは負、重み付けでは正と推定値の符号が異なっていますが、いずれも信頼区間に0を含んでおり統計的には効果なしという結論になるのでこれ以上調べる必要はないでしょう。
最後に重みのサマリ情報と標準誤差の関係について見てみましょう。全サンプルの変動係数と共変量による再調整なしのときの標準誤差との関係は以下のとおりです。
df_wbal_est_summary_ %>% ggplot(aes(x = coef.of.var_all, y = std.error_wo, group = method, color = method)) + geom_point()
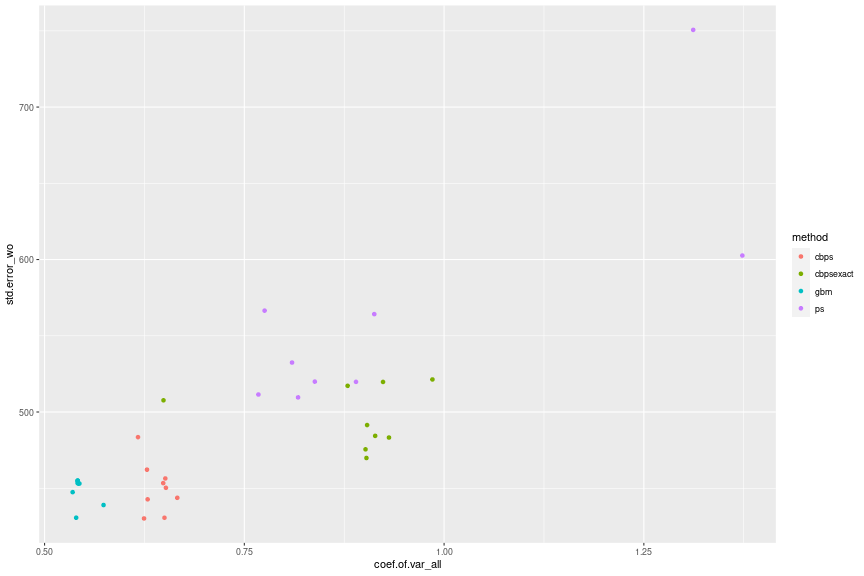
全体的に重みの変動係数が小さくなるにつれて標準誤差が小さくなることが確認できます。変動係数と標準誤差の相関は0.81です。MADや負のエントロピーについても同様の傾向が見られます。また、バランシングがうまくいっていないものも含まれるので単純比較はできませんが、手法によって変動係数の水準が異なることもわかります。GBMや過剰識別のCBPSは比較的小さく、ロジスティック回帰と丁度識別のCBPSはGBMや過剰識別のCBPSより大きく、さらにモデル依存性も強くなっています。
変動係数と共変量による再調整ありのときの標準誤差との関係は以下のとおりです。
df_wbal_est_summary_ %>% ggplot(aes(x = coef.of.var_all, y = std.error_w, group = method, color = method)) + geom_point()

共変量による再調整なしのときと比較すると、標準誤差が変動係数に依存しにくくなっていることが確認できます。
まとめ
今回は、A/Bテストができないときを想定し、共変量のバランシングを利用してATEを推定する手順を紹介しました。共変量のバランスがよくなるとモデル依存性が低下し未観測共変量の影響が小さくなりやすいことを利用して推定結果を絞り込み、推定結果の解釈を行うところまで行いました。
観察データの因果推論は難しいです。試しに何らかの推定値を計算するだけならば簡単なのですが、実務で使えるぐらいの信頼性がある結果を得るのは大変です。共変量のバランス以外にも気をつけなくてはいけないことが多いですし、細心の注意を払っても推定手法やモデルによって異なる結果が得られてしまうので結果の解釈に困ることも多いです。因果推論手法を過信して安易に使うと誤った判断を招いてしまいます。また、どのような推定方法を使うべきかについても複数の見解があり大変悩ましいです。
一方で、近年は実務家向けの研究成果やノウハウが蓄積され、ツールも整備が進み使いやすくなっています。完璧な推定値を得ようとすると大変な労力がかかりますし、データによっては不可能なこともあります。しかし、信頼区間などに基づき効果がありそうかを判断する材料の一つとして利用するのであれば有用なことが多いのではないでしょうか。
