こんにちは、リブセンスでデータサイエンティストをしている北原です。今回は小ネタで打ち切り・切断データの回帰モデルを扱います。弊社で扱っているデータの中には打ち切りデータになっているものがあり、そのようなデータから階層ベイズモデルを作ることがあります。打ち切り・切断データの扱い方が分かれば階層ベイズに拡張するのは容易なので、今回はシンプルな打ち切り回帰と切断回帰のモデルパラメータ推定のみを扱います。使う言語はStanとRです。
打ち切り回帰
正規分布
まず基本的な正規分布の打ち切りデータを扱います。
打ち切りデータというのは、ある閾値以上もしくは以下の値をとるサンプルは、存在していることはわかっても値を観測できないデータです。例えば、あるWebサイトの利用時間が一定以上のユーザーのみが使えるサービスを提供し、その利用時間をWebサイトの全利用ユーザーについて集計したものは打ち切りデータになります。入力フォームのバリデーションチェックなどで人為的に閾値を設けて収集されたデータは、打ち切りデータもしくは後で説明する切断データになっていることがよくあります。
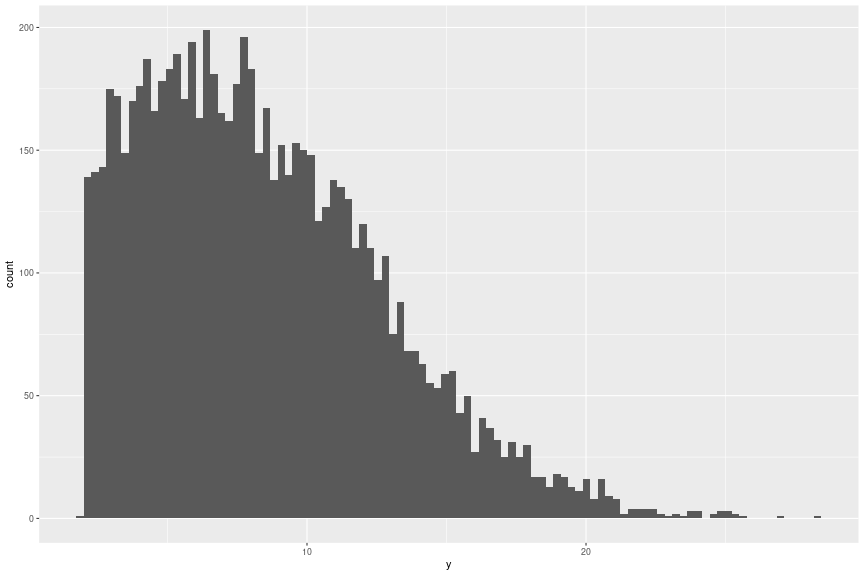
具体的には以下のようなデータです。ここでは2を打ち切りの閾値とし、打ち切り対象のサンプルは2をとるデータとしています。ヒストグラムを見ると打ち切り時にとる値にサンプルが集中した分布になっていることがわかります。
library(tidyverse) set.seed(1) n <- 10000 # 完全なデータ(正規分布) df_norm_full <- tibble( x1 = rnorm(n, mean = 1, sd = 1), x2 = rnorm(n, mean = 2, sd = 1) ) %>% mutate( y = rnorm(n, mean = 3 * x1 + 4 * x2 - 5, sd = 3) ) # 打ち切りデータ L <- 2 df_norm_cen <- df_norm_full %>% mutate( y = ifelse(y <= L, L, y) ) # ヒストグラム df_norm_cen %>% ggplot(aes(x = y)) + geom_histogram(bins = 100)

当然ながら、このような打ち切りデータを通常の線形回帰で扱おうとすると誤った推定値が得られます。
# 線形回帰 fit_lm <- lm(y ~ x1 + x2, df_norm_cen) summary(fit_lm)
Call:
lm(formula = y ~ x1 + x2, data = df_norm_cen)
Residuals:
Min 1Q Median 3Q Max
-8.7138 -1.8559 -0.1128 1.7190 10.7129
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.48479 0.06649 -22.33 <2e-16 ***
x1 2.24506 0.02681 83.74 <2e-16 ***
x2 3.05526 0.02739 111.53 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.714 on 9997 degrees of freedom
Multiple R-squared: 0.6616, Adjusted R-squared: 0.6615
F-statistic: 9771 on 2 and 9997 DF, p-value: < 2.2e-16
打ち切り回帰はこのような打ち切りを考慮したモデルです。トービットモデル(Type I )とも呼ばれます。ここでは$L$以下は打ち切られるときのモデルを扱います。切片項を含めて$n$個の回帰係数をもつ打ち切り回帰モデルは、$i$番目のサンプルの観測可能な目的変数を$y_i$、潜在変数を$y^*_i$、説明変数を${\mathbf x}_i \in {\mathbb R}^n$、回帰係数を${\mathbf \beta} \in {\mathbb R}^n$として
となります。
尤度を定式化しStanコードで記述すればパラメータの推定ができるので、尤度について考えましょう。打ち切りになっていない$y_i > L$のときは通常の線形回帰と同じです。打ち切りになっている$y_i \le L$のときは累積分布関数で表すことができます。まとめると尤度は
となります。累積分布関数は
です。Stanでは累積分布関数を使ってモデルを表現できるので、ここまでわかれば実装できます。
では、実際に実装して推定してみましょう。Stanコードは次のとおりです。累積分布関数の部分はサンプリングステートメントが使えないのでtarget記法を使う必要があります。正規分布の累積分布関数の対数はnormal_lcdf()関数で指定します。
// norm_cen.stan
data {
int<lower=0> N;
int<lower=0> M;
real L;
vector[N] y;
matrix[N, M] x;
}
parameters {
vector[M] b;
real<lower=0> s;
}
model {
vector[N] z;
z = x * b;
for (i in 1:N) {
if (y[i] > L) {
y[i] ~ normal(z[i], s);
} else {
target += normal_lcdf(L | z[i], s);
}
}
s ~ cauchy(0, 1e6);
}
呼び出しコードは次のようになります。
library(rstan) library(doParallel) registerDoParallel(detectCores()) options(mc.cores = parallel::detectCores()) stan_norm_cen.obj <- stan_model(file = "stan/norm.stan") fit_norm_cen <- sampling( stan_norm_cen.obj, data = list( N = nrow(df_norm_cen), M = ncol(df_norm_cen), L = 2, y = df_norm_cen$y, x = df_norm_cen %>% dplyr::select(x1, x2) %>% mutate(intercept = 1) ) ) summary(fit_norm_cen)$summary
結果は以下のとおりです。打ち切りを考慮することで適切な推定ができていることがわかります。
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat b[1] 2.996202 0.0007378284 0.03466783 2.927457 2.973089 2.996465 3.019794 3.062712 2207.713 1.000712 b[2] 4.048162 0.0007368771 0.03456306 3.978758 4.025448 4.048568 4.071670 4.115590 2200.059 1.000649 b[3] -5.092113 0.0021627003 0.09487830 -5.275908 -5.155265 -5.092315 -5.031110 -4.897838 1924.603 1.000927 s 3.035012 0.0004613430 0.02492723 2.986512 3.019018 3.034312 3.051607 3.084567 2919.444 1.000701 lp__ -13409.666368 0.0355435193 1.38710426 -13413.218686 -13410.314777 -13409.375607 -13408.642134 -13407.956553 1522.991 1.002893
なお、同じStanコードで最尤推定を行うこともできます。ベイズ推定がうまくいかないときに問題が尤度の記述ミスにあるかを確認するのに便利です。
fit_ml <- optimizing( stan_norm_cen.obj, data = list( N = nrow(df_norm_cen), M = ncol(df_norm_cen), L = 2, y = df_norm_cen$y, x = df_norm_cen %>% dplyr::select(x1, x2) %>% mutate(intercept = 1) )) fit_ml
$par
b[1] b[2] b[3] s
2.996214 4.048129 -5.091220 3.033720
$value
[1] -13408.83
$return_code
[1] 0
$theta_tilde
b[1] b[2] b[3] s
[1,] 2.996214 4.048129 -5.09122 3.03372
また、最尤推定を行うだけならばAERなどの既存パッケージを使ったほうが簡単です。AERパッケージのtobit()関数は対数正規分布などの打ち切りデータにも対応しています。
library(AER) tobit(y ~ x1 + x2, left = 2, data = df_norm_cen)
Call:
tobit(formula = y ~ x1 + x2, left = 2, data = df_norm_cen)
Coefficients:
(Intercept) x1 x2
-5.091 2.996 4.048
Scale: 3.034
対数正規分布
打ち切りデータは正規分布以外でも生じます。そこで非正規分布のケースについても推定してみましょう。弊社でも正規分布より非正規分布の打ち切りデータをよくみかけます。ここでは非正規分布の例として、対数正規分布を扱います。
ここでは次のようなデータを扱います。
# 完全なデータ(対数正規分布)の打ち切りデータ L <- 0.5 df_lognorm_full <- tibble( x1 = rnorm(n, mean = 1, sd = 0.5), x2 = rnorm(n, mean = 2, sd = 0.5) ) %>% mutate( y = rlnorm(n, meanlog = 2 * x1 + x2 - 5, sdlog = 3) ) # 対数正規分布の打ち切りデータ df_lognorm_cen <- df_lognorm_full %>% mutate( y = ifelse(y <= L, L, y) ) # ヒストグラム df_lognorm_cen %>% filter(y <= 50) %>% ggplot(aes(x = y)) + geom_histogram(bins = 100)

非正規分布の打ち切りデータについても、累積分布関数が使える分布であれば正規分布のときと同様に考えることで尤度を導出できます。対数正規分布の打ち切り回帰モデルでは、正規分布を対数正規分布、累積正規分布関数を累積対数正規分布関数に置き換えるだけです。
対数正規分布の打ち切り回帰モデルの推定は次のようにすればできます。
// lognorm_cen.stan
data {
int<lower=0> N;
int<lower=0> M;
real L;
vector[N] y;
matrix[N, M] x;
}
parameters {
vector[M] b;
real<lower=0> s;
}
model {
vector[N] z;
z = x * b;
for (i in 1:N) {
if (y[i] > L) {
y[i] ~ lognormal(z[i], s);
} else {
target += lognormal_lcdf(L | z[i], s);
}
}
s ~ cauchy(0, 1e6);
}
lognorm_cen_obj <- stan_model(file = "stan/lognorm.stan") fit_lornorm_cen <- sampling( lognorm_cen_obj, data = list( N = nrow(df_lognorm_cen), M = ncol(df_lognorm_cen), L = L, y = df_lognorm_cen$y, x = df_lognorm_cen %>% dplyr::select(x1, x2) %>% mutate(intercept = 1) )) summary(fit_lornorm_cen)$summary
結果は次のとおりです。適切な推定ができていることがわかります。
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat b[1] 1.943234e+00 0.001447477 0.06865837 1.807253e+00 1.895784e+00 1.944145 1.990657e+00 2.075031 2249.901 1.000124 b[2] 9.074874e-01 0.001528194 0.06485226 7.837377e-01 8.630158e-01 0.909162 9.522287e-01 1.034844 1800.914 1.004599 b[3] -4.719476e+00 0.003966194 0.15981991 -5.036319e+00 -4.828296e+00 -4.716648 -4.611292e+00 -4.415366 1623.730 1.003486 s 2.916444e+00 0.000712668 0.03361921 2.851849e+00 2.893461e+00 2.916146 2.938914e+00 2.982114 2225.361 1.002471 lp__ -1.062114e+04 0.036289859 1.40253830 -1.062476e+04 -1.062180e+04 -10620.807861 -1.062013e+04 -10619.387912 1493.685 1.000836
切断回帰
切断データは、ある閾値以上もしくは以下の値をとるサンプルのみのデータです。打ち切りデータで打ち切り対象になったサンプルを除外したデータと同じです。何らかの条件を満たしたときしか収集していないデータは切断データになっていることが多いです。ここでは正規分布の切断データを扱います。
具体的には次のようなデータです。
# 切断データ(正規分布) L <- 2 df_norm_trunc <- df_norm_full %>% filter(y > L) # ヒストグラム df_norm_trunc %>% ggplot(aes(x = y)) + geom_histogram(bins = 100)
切断回帰の尤度は条件付き確率
からわかります。
コードは次のようになります。$P(y_i > L \mid {\mathbf x}_i)$は累積分布関数を使わなくともnormal_lccdf()関数を使うことで指定できます。
// norm_trunc.stan
data {
int<lower=0> N;
int<lower=0> M;
real L;
vector[N] y;
matrix[N, M] x;
}
parameters {
vector[M] b;
real<lower=0> s;
}
model {
vector[N] z;
z = x * b;
for (i in 1:N) {
y[i] ~ normal(z[i], s);
target += -normal_lccdf(L | z[i], s);
}
s ~ cauchy(0, 1e6);
}
stan_norm_trunc.obj <- stan_model(file = "stan/norm_trunc.stan") fit_norm_trunc <- sampling( stan_norm_trunc.obj, data = list( N = nrow(df_norm_trunc), M = ncol(df_norm_trunc), L = 2, y = df_norm_trunc$y, x = df_norm_trunc %>% dplyr::select(x1, x2) %>% mutate(intercept = 1) ) ) summary(fit_norm_trunc)$summary
結果は次のとおりです。適切に推定できていることがわかります。
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat b[1] 3.012877 0.0011430840 0.04672983 2.922775 2.980975 3.012651 3.043085 3.107331 1671.214 1.000609 b[2] 4.015083 0.0014372637 0.05123402 3.915150 3.981242 4.014829 4.048834 4.120169 1270.703 1.001691 b[3] -5.036700 0.0051398114 0.16847732 -5.375641 -5.145249 -5.034812 -4.922481 -4.707501 1074.456 1.001350 s 3.041773 0.0006862641 0.03068500 2.982469 3.021232 3.042104 3.061523 3.103943 1999.263 1.001006 lp__ -10494.299790 0.0344773283 1.36769986 -10497.695133 -10495.042765 -10493.984945 -10493.258194 -10492.568835 1573.673 1.001879
Stanは切断分布をサポートしているので、さらに簡潔な表記が可能です。次のようにサンプリングステートメントの末尾で切断範囲を指定します。
// norm_trunc2.stan data { int<lower=0> N; int<lower=0> M; real L; vector[N] y; matrix[N, M] x; } parameters { vector[M] b; real<lower=0> s; } model { vector[N] z; z = x * b; for (i in 1:N) { y[i] ~ normal(z[i], s) T[L,]; } s ~ cauchy(0, 1e6); }
当然ながらほぼ同じ推定結果が得られます。
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat b[1] 3.011582 0.001179636 0.04579857 2.920585 2.980081 3.011699 3.043146 3.100901 1507.328 1.001271 b[2] 4.014519 0.001323741 0.05071257 3.912309 3.980963 4.013553 4.048705 4.113432 1467.659 1.000982 b[3] -5.032630 0.004866510 0.16886615 -5.361202 -5.147676 -5.032737 -4.919485 -4.697018 1204.065 1.001550 s 3.041190 0.000642647 0.03197297 2.980695 3.019259 3.040462 3.062015 3.106482 2475.260 1.001484 lp__ -10494.306119 0.036866354 1.41487956 -10497.940524 -10495.008916 -10493.973515 -10493.265066 -10492.569499 1472.918 1.002343
まとめ
今回は打ち切り・切断データの回帰モデルのパラメータ推定について扱いました。Stanではモデルの指定に累積分布関数や切断分布を使うことができるので、打ち切り・切断回帰のパラメータ推定を容易に行うことができます。そのため、打ち切り・切断回帰の階層ベイズモデルなども比較的簡単に作ることができます。
