線形回帰のギブスサンプリング - Bayesian Factorization Machinesのバイアス項の実装 -

　こんにちは、リブセンスでデータサイエンティストをしている北原です。今回から何回かに渡ってBayesian Factorization Machines（BFM）関連の記事を書いていこうと思います。まずは、基本となる連続値を目的変数としたBFMのギブスサンプリング実装について、3回に分けて説明します。BFMの技術要素は、(1)線形モデルのギブスサンプリング、(2)階層ベイズ、(3)交互作用項の高速計算から成り立っており、それぞれバイアス項、ハイパーパラメータ、交互作用項の実装に対応しています。今回はその中の(1)を扱います。コードはJuliaです。なお、本記事は、協調フィルタリング用Factorization Machines（FM）とベイズ統計について、ある程度知識がある方が読むことを想定しています。これらについては検索すると多くの解説記事が見つかるので、詳しくはそちらをご参照ください。

動機

　初回なので、なぜBayesian Factorization Machines（BFM）を使うのかということについて説明しようと思います。

　機械学習を使った施策を成功させるには、KPI向上の阻害要因を見つけて適切な課題設定をすることが一番重要で、その次に課題を解決できるデータや手法を導入できるかが重要になります。課題が明確でそこを狙い撃ちできるデータや手法を導入できたときはうまくいくことが多いです。しかし、課題が不明瞭なまま高精度と評判の技術を導入しただけではうまくいかないことが多いです。主力事業に共通の課題もありますが、事業内容や事業フェーズによって生じる課題は異なるので、データやモデルを調整することで個別の課題に柔軟に対処できる手法があると便利です。さらに、安定性が高くモデルの調整負担や計算負荷が低いと利用しやすくなります。そのような手法として着目していたのがBFMです。

　BFMにはFactorization Machines（FM）としての特長とベイズモデルとしての特長があります。FMには、(1)ユーザー固有の情報と副次情報の双方を反映できる、(2)モデルの表現能力が高いのに比較的シンプル、という特長があります。FMは、表現能力の高さに起因して、学習データへのオーバーフィットが生じやすいですが、BFMはベイズモデルとすることでこの問題が生じにくくなっています。ベイズモデルとすることで(3)推定の安定性の向上と、(4)パラメータ調整負担の軽減が図られ、(5)拡張性も高くなっています。

ユーザー固有の情報と副次情報の双方を反映可能

　ユーザー固有の情報と副次情報の双方を反映できることで、コールドスタート問題に対応でき、特徴量を活用した課題解決もしやすくなります。

　協調フィルタリングを使うとサービス利用が増えるほどレコメンデーション精度を向上させられるものの、通常の協調フィルタリングでは、評価データがないと推論ができないですし、評価データが少ないほど精度が低下するというコールドスタート問題が生じます。リブセンスは人材系サービスが主力事業ですが、人材系サービスはサービス品質が向上するほどユーザー一人あたりの利用期間は短くなると考えられます。例えば、よい求人がすぐに見つかるようになれば求職活動期間は平均的に短くなります。そのため、サービス利用が増えるほど精度が向上するという特長を維持しつつも、評価データがないあるいは少ないユーザーにおいても精度を維持するというのが、弊社におけるレコメンデーション技術の共通課題となっています。　

　FMを使うことで、評価データが少ないユーザーには副次情報を使ったレコメンドを行い、評価データが増えるにつれてパーソナライズされたレコメンドを行うことができます。協調フィルタリングとコンテンツベースレコメンデーションを併用することで同様のことを行えます。しかし、二つを同時期に使うと冗長なレコメンドが増えユーザービリティが低下します。評価データ量に応じて二つの手法を切り替えれば冗長性は低下させられるものの、各手法個別でのモデル調整に加え、切り替えタイミングの最適化などが必要になります。FMを使えば、手法の切り替えなどを意識しなくとも、評価データ数に応じたレコメンドが可能になります。

　レコメンデーションに利用する特徴量を活用することで、様々な施策を行うことができます。例えば、Bag of Wordsなどの過去の評価アイテム情報をユーザー属性データとして使うとコンテンツベースレコメンデーションと同じことができます。また、以前の記事でも紹介したように、転職サイトで希望勤務地外の求人をレコメンドするのに利用したこともあります。例えば、希望勤務地が神奈川の人は、希望勤務地に東京都を指定していなくても勤務地以外の条件が合っていれば勤務地が東京都であってもレコメンドしたほうがよいことがあります。このような勤務地の関係性をルールベースで管理するのは大変ですが、FMを使えば希望勤務地と勤務地の関係性に加え、その他の求人情報も考慮したレコメンドができます。また、利用情報が増えると、ユーザーと勤務地の関係性も学習されてパーソナライズされたレコメンドができるようになります。つまり、利用が増えてくると、希望勤務地が神奈川の人であっても、勤務地が神奈川の求人しか興味がない人には神奈川の求人をレコメンドし、東京都の求人にも興味がありそうな人には神奈川だけでなく東京都の求人も含めてレコメンドできるわけです。

高い表現能力とシンプルさを両立

　表現能力が高いのに比較的シンプルなモデルになっているため、工夫すると計算量を削減可能な部分が多く、コストパフォーマンスに優れています。

　FMの表現能力の高さは、元論文や、それを実装したlibFMの論文でも示されているように、既存の多くの協調フィルタリングを含んだモデルになっていることからわかります。また、前節でも少し紹介しているように、特徴量を工夫することで様々なレコメンデーションが可能になるという特長があります。

　しかし、表現能力の高いモデルは複雑で多くの計算機リソースを要することが多いという問題があります。高コストな手法はコストを上回る事業貢献の見込みがないと使いにくく、多少精度がよい程度では不十分です。そういう意味で、深層学習系の協調フィルタリングはまだコスパが悪く使いにくい印象です。

　FMも何も工夫をしないと計算量は比較的多いものの、データ構造やアルゴリズムの工夫によって学習時、推論時ともに計算量を削減できることが知られています。ハードウェアの増強に頼らず、計算量を削減できるのは大きなメリットです。ただし、副次情報を使うほどメモリ使用量は増えますし、非ゼロ要素のデータが増えるほど計算量も増えるので、使える副次情報の量は計算機リソースに依存します。実際のところ、Matrix Factorizationのような協調フィルタリング手法を余裕をもって運用できるだけの計算機リソースがあるなら、計算量やメモリ使用量が問題になることは少ないです。

安定した推定が可能

　ベイズ推定によって、学習データへのオーバーフィット抑制や、平均からかけ離れたユーザーやアイテムに起因する異常値出力の抑制ができます。

　FMは学習データにオーバーフィットしやすいモデルなので、ベイズ推定によって明確な精度向上が得られることが多いです。評価データが少ないユーザーやアイテムではオーバーフィットによる精度低下が生じやすいので、コールドスタート問題の緩和にも寄与しています。

　平均からかけ離れた特徴をもつユーザーやアイテムがあると異常値を出力してしまうことがありますが、ベイズ推定を利用することでこのようなことを抑制することもできます。異常値に基づいたレコメンデーションがクレームにつがなることもありうるので、利用場面によっては大きなメリットになります。

パラメータ調整が容易

　正則化係数に相当するパラメータを自動的に推定できる階層ベイズモデルにすることで、パラメータ調整負担を軽減させることができます。そのため、精度に大きく影響する調整パラメータは因子数のみになります。

　ユーザーの行動やアイテムの特徴が徐々に変化していきモデルを調整する必要があることがありますが、調整パラメータが多いと検証に手間がかかります。ベイズ最適化などを利用してパラメータ調整を自動化することもできますが、計算時間が増加するなど運用負担が増えます。

　一方で階層ベイズを使ったBFMでは、指定した因子数に応じて正則化係数に相当するパラメータが自動調整されるので、ユーザーの行動やアイテムの特徴が多少変化しても精度が低下しにくく、頻繁な再調整が不要になります。変化が大きい場合はパラメータ調整が必要になりますが、その場合も因子数と精度の関係は単調になることが多いので調整は容易です。

拡張性が高い

　ベイズ統計モデルの知見を部分的に導入するなどしてモデル構造をカスタマイズしたり、ベイズモデルの特徴を活かして課題解決を図ることができることが期待できます。

　どのようなカスタマイズが必要になるかは課題に依存しますが、不均衡データへの対応や一部の人気アイテムにレコメンデーションが集中する問題などへの対応が考えられます。例えば、BFMをThompson Samplingに使えば、人気アイテムへの集中を回避できるとともに、より有効なアイテムを探索するレコメンデーションが実現できるのではと考えています。

モデル

　今回はシンプルな線形回帰モデルを考えます。条件付き分布を導出できるように事前分布には共役事前分布を使います。

　線形回帰モデルは、$M$個の特徴量をもつ$N$個の観測データがあるときに$i$番目の目的変数を$y_i \in {\mathbb R}$、説明変数を${\bf x}_i \in {\mathbb R}^{M}$、回帰係数を$w_0 \in {\mathbb R}$、${\bf w} \in {\mathbb R}^M$として

$$ \begin{eqnarray} y_i &=& w_0 + \sum^M_{j=1}{w_j x_{i,j}}\label{eq:lm} \end{eqnarray} $$

と表します。また、$y$の推定値は$\hat{y}(\mathbf{x}_i, \mathbf{w}, w_0)$で表します。各パラメータの分布は分散の逆数を$\alpha$として

$$ \begin{eqnarray} P(y_i | \mathbf{x}_i, \mathbf{w}, w_0, \alpha) &=& \mathcal{N} \bigl(y_i | w_0 + \sum^M_{j=1}{w_j x_{i,j}, \alpha^{-1}} \bigr) \\ P(w_j) &=& \mathcal{N} (w_j | \mu, \lambda) \\ P(\alpha) &=& Gam (\alpha | \alpha_0, \beta_0) \end{eqnarray} $$

とします。今回は$\mu$、$\lambda$、$\alpha_0$、$\beta_0$は定数です。$\mathcal{N}(\mu, \lambda^{-1})$は$\mu$を平均、$\lambda$ を分散の逆数とした正規分布、$Gam(\alpha, \beta)$は$\alpha$と$\beta$をパラメータとしたガンマ分布で、正規化定数を無視すると次のようになります。

$$ \begin{eqnarray} \mathcal{N}(x | \mu, \lambda^{-1}) &\propto& \lambda^{\frac{1}{2}} \exp \Bigl(-\frac{1}{2} \lambda (x - \mu)^2\Bigr)\\ Gam(x | \alpha, \beta) &\propto& x^{\alpha - 1} \exp(-\frac{x}{\beta}) \end{eqnarray} $$

このモデルはBFMのハイパーパラメータの設定と交互作用項を削除したものと同じです。 プレート表現は次のようになります。

線形回帰モデルのプレート表現

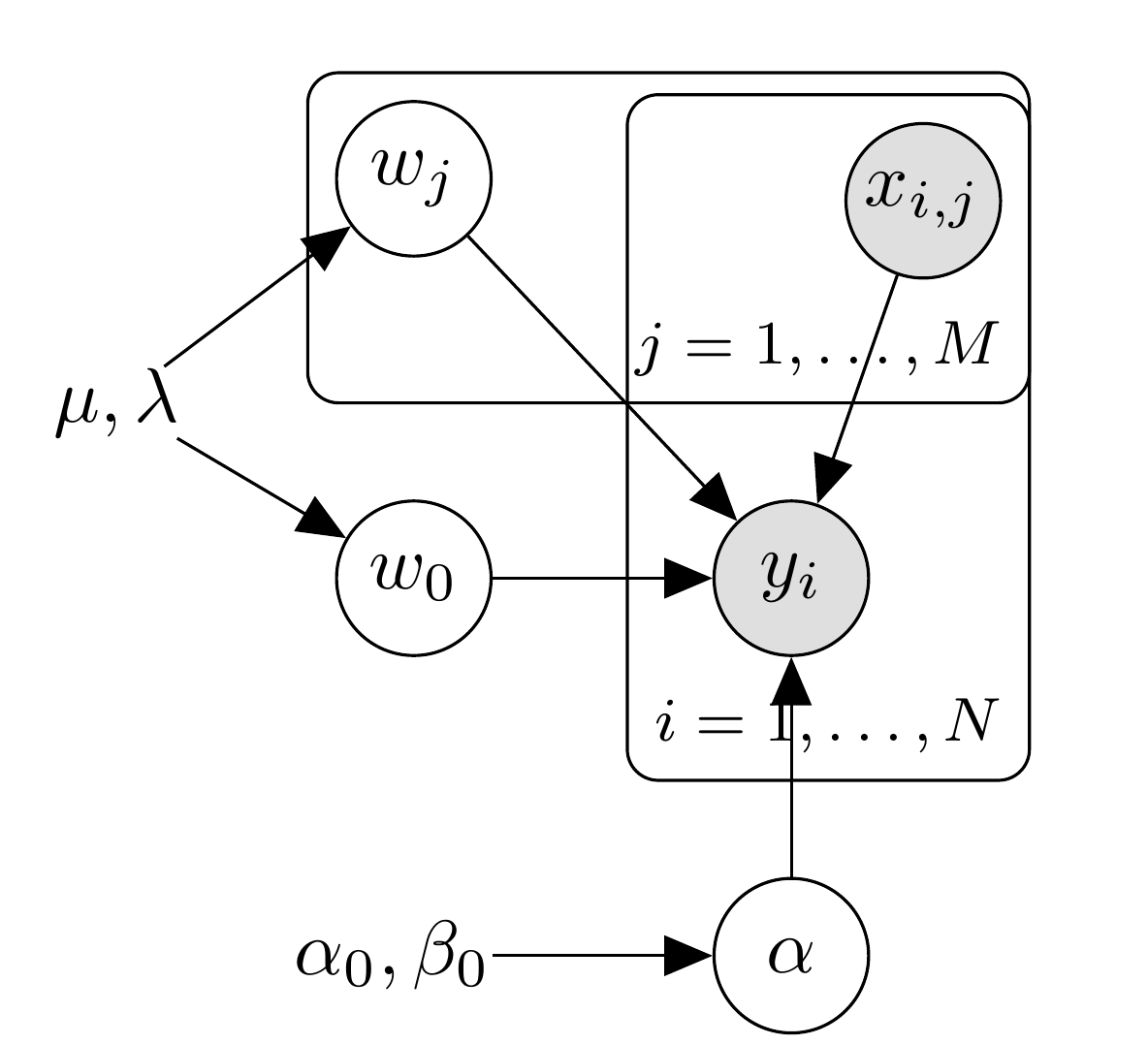
条件付き分布

　ギブスサンプリングでは条件付き分布にしたがって順次各パラメータのサンプリングを行うので、条件付き分布を導出します。初回なので丁寧にやりましょう。

　まず、分散の逆数$\alpha$の条件付き分布を導出します。データ数は$N$とします。正規化定数に含まれてしまう部分は無視し、$\alpha$による関数形状に関わる部分にのみ着目すると

$$ \begin{eqnarray} P(\alpha| y_1, &\dots&, y_N, \mathbf{x}_1,\dots, \mathbf{x}_N, \mathbf{w}, w_0) \nonumber \\ &\propto& P(\alpha) P(w_0) \prod_{j=1}^M P(w_j) \prod_{i=1}^N P(y_i | \mathbf{x}_i, \mathbf{w}, w_0, \alpha) \nonumber \\ &\propto& P(\alpha) \prod_{i=1}^N P(y_i | \mathbf{x}_i, \mathbf{w}, w_0, \alpha) \nonumber \\ &=& Gam(\alpha | \alpha_0, \beta_0) \prod_{i=1}^N \mathcal{N}(y_i | \hat{y}(\mathbf{x}_i, \mathbf{w}, w_0), \alpha) \nonumber \\ &\propto& \alpha^{\alpha_0 - 1} \exp \Bigl(-\frac{\alpha}{\beta_0} \Bigr) \prod_{i=1}^N \alpha^{\frac{1}{2}} \exp \Bigl( -\frac{1}{2} \alpha (y_i - \hat{y}(\mathbf{x}_i, \mathbf{w}, w_0))^2 \Bigr) \nonumber \\ &\propto& \alpha^{\alpha_0 + \frac{N}{2} - 1} \exp \Bigl( - \alpha \Bigl( \frac{1}{\beta_0} + \frac{1}{2}\sum_{i=1}^N (y_i - \hat{y}(\mathbf{x}_i, \mathbf{w}, w_0))^2 \Bigr) \Bigr) \nonumber \\ &\propto& Gam\Bigr(\alpha_0 + \frac{N}{2}, \Bigl( \frac{1}{\beta_0} + \frac{1}{2}\sum_{i=1}^N (y_i - \hat{y}(\mathbf{x}_i, \mathbf{w}, w_0))^2 \Bigr)^{-1} \Bigr) \end{eqnarray} $$

となります。

　同様に、$l$番目の回帰係数$w_l$​の条件付き分布は

$$ \begin{eqnarray} P(w_l| y_1, &\dots&, y_N, \mathbf{x}_1,\dots, \mathbf{x}_N, \mathbf{w} \backslash \{w_l\}, w_0, \alpha) \nonumber \\ &\propto& P(w_l | \mu, \lambda) \prod_{i=1}^N P(y_i | \mathbf{x}_i, \mathbf{w}, w_0, \alpha) \nonumber \\ &=& \mathcal{N}(w_l | \mu, \lambda) \prod_{i=1}^N \mathcal{N}(y_i | \hat{y}(\mathbf{x}_i, \mathbf{w}, w_0), \alpha) \nonumber \\ &\propto& \exp \Bigl(-\frac{1}{2} \lambda (w_l - \mu)^2 \Bigr) \prod_{i=1}^N \exp \Bigl(- \frac{1}{2} \alpha (y_i - \hat{y}(\mathbf{x}_i, \mathbf{w}, w_0))^2 \Bigr) \nonumber \\ &=& \exp \Bigl( -\frac{1}{2} \lambda (w_l - \mu)^2 - \frac{1}{2} \alpha \sum_{i=1}^N (y_i - w_0 - \sum^M_{j=1, j \ne l}{w_j x_{i,j}} - w_l x_{i, l})^2 \Bigr) \nonumber \\ &\propto& \exp \Bigl( -\frac{1}{2} \lambda (w_l^2 - 2 \mu w_l) - \frac{1}{2} \alpha \Bigl( \Bigl( \sum_{i=1}^N x_{i,l}^2 \bigr) w_l^2 - 2 \sum_{i=1}^N x_{i, l} \bigl(y_i - w_0 - \sum^M_{j=1, j \ne l}{w_j x_{i,j}} \bigr) w_l \Bigr) \Bigr) \nonumber \\ &=& \exp \Bigl( -\frac{1}{2} \Bigl \{ (\lambda + \alpha \sum_{i=1}^N x_{i,l}^2)w_l^2 - 2 \bigl( \mu \lambda + \alpha \sum_{i=1}^N x_{i, l} \bigl(y_i - w_0 - \sum^M_{j=1, j \ne l}{w_j x_{i,j}} \bigr) \bigr) w_l \Bigl\}\Bigr) \nonumber \\ &\propto& \exp \Bigl( -\frac{1}{2} \Bigl \{ (\lambda + \alpha \sum_{i=1}^N x_{i,l}^2) \Bigl( w_l - (\lambda + \alpha \sum_{i=1}^N x_{i,l})^{-1} \bigl( \mu \lambda + \alpha \sum_{i=1}^N x_{i, l} \bigl(y_i - w_0 - \sum^M_{j=1, j \ne l}{w_j x_{i,j}} \bigr) \bigr) \Bigr)^2 \Bigl\}\Bigr) \nonumber \\ &\propto& \mathcal{N} \Bigr((\lambda + \alpha \sum_{i=1}^N x_{i,l}^2)^{-1} \bigl( \mu \lambda + \alpha \sum_{i=1}^N x_{i, l} \bigl(y_i - w_0 - \sum^M_{j=1, j \ne l}{w_j x_{i,j}} \bigr), (\lambda + \alpha \sum_{i=1}^N x_{i,l}^2)^{-1} \Bigr) \end{eqnarray} $$

となります。なお、$\mathbf{w}$から$w_l$のみを除いたものを$\mathbf{w} \backslash \{w_l\}$と表記しています。

　簡単なモデルなのに表記が煩雑なので、モデルの表記を少し変更しましょう。ブロック化しないギブスサンプリングでは一変数ずつサンプリングを行うので、サンプリング対象ではない変数は定数として扱うことができます。そこで、サンプリング対象の変数を$\theta$とし、$\theta$に乗じている部分と残りの部分に分けて表記します。$\theta$に乗じている部分と残りの部分はデータ$\mathbf{x}$に依存するので、$i$番目のデータについてそれぞれ$h_{\theta}(\mathbf{x}_i)$、$g_{\theta}(\mathbf{x}_i)$と表記します。まとめると

$$ \begin{eqnarray} \hat{y}(\mathbf{x}_i, \theta) &=& g_{\theta}(\mathbf{x}_i) + \theta h_{\theta}(\mathbf{x}_i) \label{eq:gh} \\ \theta &=& w_l \label{eq:theta} \\ g_{\theta}(\mathbf{x}_i) &=& w_0 + \sum^M_{j=1, j \ne l}{w_j x_{i,j}} \\ h_{\theta}(\mathbf{x}_i) &=& x_{i, l} \end{eqnarray} $$

となります。この表記を使うと、$l$番目の係数$\theta=w_l$​をサンプリングするときの条件付き分布は

$$ \begin{eqnarray} P(w_l| y_1, &\dots&, y_N, \mathbf{x}_1,\dots, \mathbf{x}_N, \mathbf{w} \backslash \{w_l\}, w_0, \alpha) \nonumber \\ &\propto& \mathcal{N} \Bigr((\lambda + \alpha \sum_{i=1}^N h_{\theta}(\mathbf{x}_i)^2)^{-1} \bigl( \mu \lambda + \alpha \sum_{i=1}^N h_{\theta}(\mathbf{x}_i) \bigl(y_i - g_{\theta}(\mathbf{x}_i)\bigr), (\lambda + \alpha \sum_{i=1}^N h_{\theta}(\mathbf{x}_i)^2)^{-1} \Bigr) \end{eqnarray} $$

と表現できます。また、$\theta=w_0$の場合、$h_{\theta}(\mathbf{x}_i) = 1$、$g_{\theta}(\mathbf{x}_i) = \sum^M_{j=1}{w_j x_{i,j}}$と置き換えることで同じ条件付き分布が得られます。サンプリングする変数が変わると$\theta$が変わりますし、データ$\mathbf{x}$が変わると$h_{\theta}(\mathbf{x}_i)$と$g_{\theta}(\mathbf{x}_i)$も変わりますが、統一的に表記できます。次節では、この表記を使って線形回帰を実装しましょう。

実装

　それでは実装してみましょう。今回は式との対応関係がわかりやすいようにあえて冗長な書き方をします。

　式($\ref{eq:lm}$)を使って推定値$\hat{y}(\mathbf{x}_i, \theta)$を計算すると回帰係数のサンプリングのたびに$O(M)$の計算が必要となるため、少しだけ実装上の工夫をして計算量を$O(1)$にします。具体的には、あらかじめ$\hat{y}(\mathbf{x}_i, \theta)$を計算しておき、更新されたモデルパラメータの差分のみを更新します。式($\ref{eq:gh}$)、式($\ref{eq:theta}$)の表記を使い、更新後のモデルパラメータを$\theta^{\ast}$、更新前のモデルパラメータを$\theta$と表記します。このとき更新後の推定値$\hat{y}(\mathbf{x}_i, \theta^{\ast})$​は

$$ \begin{eqnarray} \hat{y}(\mathbf{x}_i, \theta^{\ast}) = \hat{y}(\mathbf{x}_i, \theta) + (\theta^{\ast} - \theta) h_{\theta}(\mathbf{x}_i) \end{eqnarray} $$

となります。

　線形回帰モデルのギブスサンプリングの関数は以下のようになります。初期値は$w_0$と$\mathbf{w}$は0、$\alpha$は1としています。そのため、$\hat{y}(\mathbf{x}_i, \theta)$の初期値も0となっています。また、定数は$\mu=0$、$\lambda = \alpha_0 = \beta_0 = 1$としています。

using Distributions
using Random

function lm_gs(y, x, n_sample, seed=1)
    Random.seed!(seed)
    N = size(x)[1]  # データ数
    M = size(x)[2]  # 特徴量数

    # モデルパラメータ
    w₀ = zeros(Float64, n_sample)
    w = zeros(Float64, M, n_sample)
    α = ones(Float64, n_sample)

    # 推定値（回帰係数の初期値を全て0にしているので0）
    ŷ = zeros(Float64, N)

    # 定数
    μ = 0.0
    λ = 1.0
    α₀ = 1.0
    β₀ = 1.0

    for s in 2:n_sample
        θ = w₀[s-1]
        h = ones(Float64, N)
        g = ŷ .- θ

        σ̃² = calc_var(α[s-1], λ, h)
        μ̃ = calc_mean(y, g, h, σ̃², α[s-1], μ, λ)
        w₀[s] = rand(Normal(μ̃, sqrt(σ̃²)))
        ŷ .+= update_y(w₀[s], w₀[s-1], h)

        for j in 1:M
            θ = w[j, s-1]
            h = x[:,j]
            g = ŷ .- θ .* h

            σ̃² = calc_var(α[s-1], λ, h)
            μ̃ = calc_mean(y, g, h, σ̃², α[s-1], μ, λ)
            w[j, s] = rand(Normal(μ̃, sqrt(σ̃²)))
            ŷ .+= update_y(w[j, s], w[j, s-1], h)
        end

        α[s] = rand(Gamma(α₀ + 0.5 * N, 1 / (1/β₀ + 0.5 * sum((y .- ŷ).^2))))
    end
    return w, w₀, α
end

function calc_var(α, λ, h)
    1 / (λ + α * sum(h.^2))
end

function calc_mean(y, g, h, σ̃², α, μ, λ)
    (μ * λ + α * sum(h .* (y .- g))) * σ̃²
end

function update_y(θᵃ, θ, h)
    (θᵃ - θ) .* h
end

　実行コードと出力は以下のようになります。精度はともかく、推定できていることが確認できると思います。

N =1000
w = collect(1:3)
w₀ = 4
α = 3

Random.seed!(123)
X = rand(Normal(0, 1), N, length(w))
y = rand.(Normal.(X * w .+ w₀ , sqrt(1/α)))

w, w₀, α = lm_gs(y, X, 1000)
@show mean(w₀[10:end])
@show mean(w[:,10:end], dims = 2)
@show mean(α[10:end])

mean(w₀[10:end]) = 3.9742487970133342
mean(w[:, 10:end], dims = 2) = [1.0232580311535553; 2.005438652874803; 3.012807504788296;;]
mean(α[10:end]) = 2.789578742000532

まとめ

　BFMのギブスサンプリング実装解説の初回として、線形回帰モデルのギブスサンプリング実装について説明しました。今回の実装内容は、BFMのバイアス項の実装とほぼ同じになっています。次回はハイパーパラメータ部分の実装について解説します。