こんにちは、リブセンスでデータサイエンティストをしている北原です。今回はアウトカムが2値のHeterogeneous Treatment Effects(HTE)に関する簡単な検証実験を扱います。コードはRです。やりたいことはパラメトリックなモデルのみを使ってHTEを推定することですが、比較用に非線形モデルを使った方法についても調べました。
Heterogeneous Treatment Effects(HTE)
HTEは、属性等で条件づけた各サンプルの因果効果です。Average Treatment Effects(ATE、平均処置効果)は平均したものなのでデータ全体で一つ得られますが、HTEはサンプルごとに計算されます。
HTEを正確に推定するのは難しいです。過去記事でも扱ったように、ATEですら安定した推定結果が得られません。そのため、効果検証で利用するより、予測などと同じように極端に正確でなくとも問題ない場面で利用するのが適しています。
実務上どのような場面で使えるかというと、KPIのアップリフトなどで使うことができます。次のような特徴をもつ施策で有効です。
- 一部のユーザーにしか実施できない(実施コストがかかる、実施リソースが限られている等)
- 施策の効果がユーザー属性に依存する
検証内容
今回の簡易検証も対象ユーザー数が限定された施策がきっかけで、検証内容もその施策の問題設定を踏まえたものになっています。この施策では、KPIが2値の比率なので今回の検証でもアウトカムは2値です。また、実装上の都合により、HTEを算出するのに使える演算は加減乗除でシンプルに表現できるものに限定されています。そのため、使えるモデルはパラメトリックなモデル、アルゴリズムはそれらのモデルを組み合わせるだけでHTEを算出できるものしか使えません。
2値アウトカムのHTEの特徴は上限と下限があることです。アップリフトを考えた場合、特に上限があるところがポイントです。施策がどんなにうまくいってもKPIが100%を超えることはないので、施策未実施時のKPIが大きいとHTEは小さくなりやすくなります。これは簡単な例で確認するとよくわかります。
実装上の制約を満たすアルゴリズムとしてロジスティック回帰をベース学習器としたMetalearnerを使っています。今回の問題設定ではツリータイプのアルゴリズムは使えないし、代表的なMetalearnerであるX-LearnerやR-Learnerも使えません。そのため、S-LearnerとT-Learnerを使っています。ただし、比較用にRandomforestベースのS-Learner、T-Learner、X-LearnerとGeneralized Random Forest(GRF)についても調べています。Metalearnerの各アルゴリズムについては、検索すれば解説記事が見つかるのでそちらをご覧ください。
検証の目的は、2値アウトカムHTE推定問題や各アルゴリズムの基本的な特徴を簡単な例で把握することです。実運用すると最初はうまく機能していた手法がうまくいかなくなったりすることがありますが、基本的な特徴を把握しているとそういうときの問題解決に役立ちます。
検証における着目点は、HTEの大きさと処置比率です。HTEが小さくなるほど、処置比率が50%から乖離するほど、正確な推定は難しくなることが予想されます。現実的には効果の高い施策ほどコストがかかりやすく処置比率が低くなることが多いので、これらの影響を把握しておくと施策の選定にも役立ちます。
データ
共変量は1つとし、簡単なHTEを設定してデータを作成します。処置効果は共変量に依存し、HTEはシグモイドの差分として設定します。処置比率がおおむね1割、3割、5割となる3種類のケースについて調べます。さらに3種類の処置比率のケースについて、処置効果の大きさのパラメータ5つについて調べます。5つのうち3つは共変量が大きくなるほどHTEが大きめになり、残り2つでは小さくなるように設定にします。
サンプルデータ作成コードは以下の通りです。
library(tidyverse) library(randomForest) library(grf) set.seed(1) sig <- function(x) { 1 / (1 + exp(-x)) } make_data <- function( z_p, # 処置比率のパラメータ t_p, # 処置効果の大きさのパラメータ N = 1000) { # 共変量(1つ) x <- runif(n = N, min = -1, max = 1) # 処置 s_z <- z_p + 2 * x z <- rbernoulli(n = N, p = sig(s_z)) %>% as.integer() # 処置効果の大きさ tr <- t_p * x # 結果変数 s_y <- 0.1 + tr * z + 5 * x y <- rbernoulli(n = N, p = sig(s_y)) %>% as.integer() # HTE hte <- sig(0.1 + tr + 5 * x) - sig(0.1 + 5 * x) tibble(x, z, tr, y, hte) } # 処置比率のパラメータ z_ratio_parameter <- c(0, -1.1, -2.6) z_ratio_caption <- c("処置5割", "処置3割", "処置1割") # 処置効果の大きさのパラメータ tr_parameter <- c(9, 4, 1, -1, -2) # サンプルデータセット d <- tibble(id = 1, z_ratio_parameter, z_ratio_caption) %>% full_join(tibble(id = 1, tr_parameter), by = "id") %>% select(-1) %>% mutate(id = 1:n()) %>% select(id, z_ratio_parameter, z_ratio_caption, tr_parameter) %>% mutate(data = map2(z_ratio_parameter, tr_parameter, make_data)) # 処置の比率 d %>% mutate(ratio = map(data, ~ mean(.$z))) %>% unnest(ratio) %>% group_by(z_ratio_parameter, z_ratio_caption) %>% summarise(mean_z_ratio = mean(ratio)) # z_ratio_parameter z_ratio_caption mean_z_ratio # <dbl> <chr> <dbl> # 1 -2.6 処置1割 0.107 # 2 -1.1 処置3割 0.286 # 3 0 処置5割 0.499
推定対象となるHTEをプロットすると次のようになります。上部の数値は処置効果の大きさのパラメータです。
d %>% filter(z_ratio_parameter == 0) %>% unnest(data) %>% ggplot(aes(x = x, y = hte)) + geom_point() + facet_grid(. ~ tr_parameter)
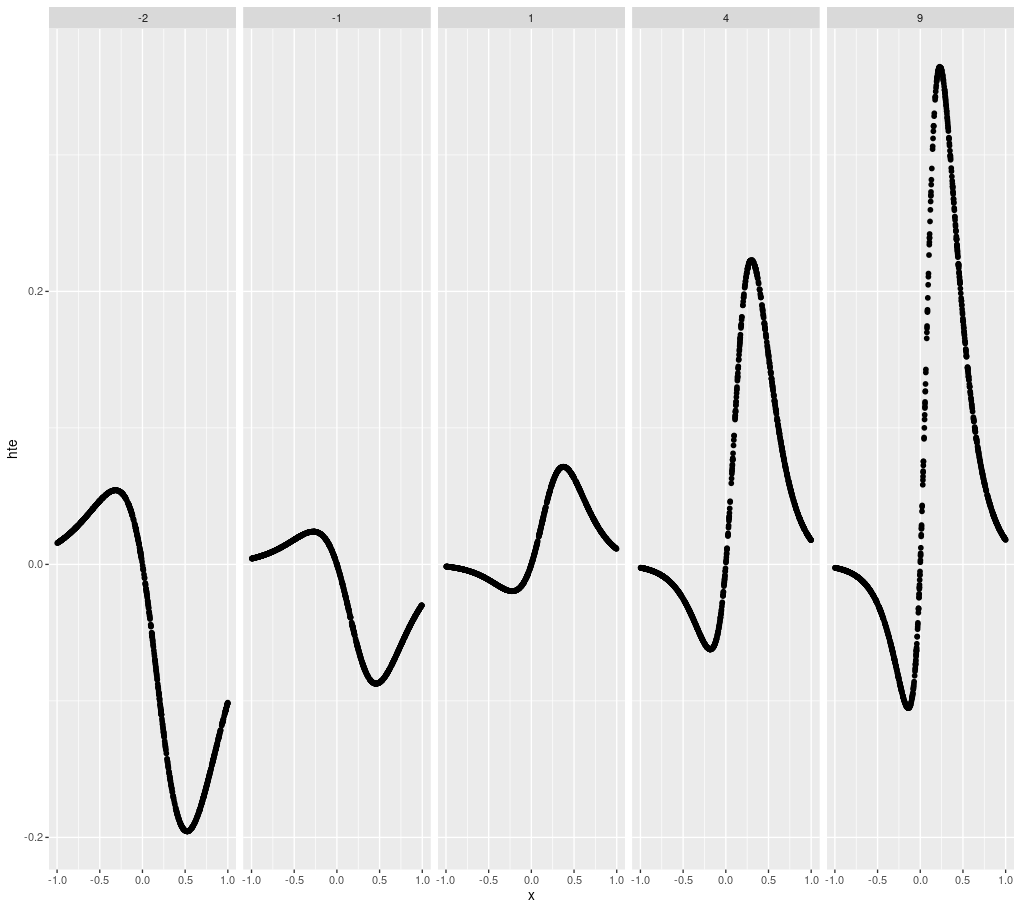
シグモイドの差としてHTEを設定しているので、共変量が十分大きいもしくは小さいとHTEの絶対値が小さくなります。例えば、処置を行わなくともアウトカムが1になる確率が高い場合、確率が1を超えることはないため処置を行なってもアウトカムが1になる確率はほとんど増えないので、HTEが小さくなります。
HTEの推定結果
事前に、指定したアルゴリズムを使ってHTEを算出しグラフをプロットする関数を定義しておきます。
# HTEを計算してプロットする関数 plot_hte <- function(dat, learner_func, title_text) { dat %>% mutate(est = map(data, learner_func)) %>% mutate(data_est = map2(data, est, ~ mutate(.x, 推定結果 = .y))) %>% unnest(data_est) %>% rename(正解 = hte) %>% pivot_longer(cols = c(正解, 推定結果), names_to = "type", values_to = "HTE") %>% ggplot(aes(x = x, y = HTE, group = type, color = type)) + geom_point() + facet_grid(z_ratio_caption ~ tr_parameter) + ggtitle(title_text) }
S-Learner
ロジスティック回帰ベースのS-Learnerの推定結果は次のようになります。
s_learner_lr <- function(d) { m <- glm(y ~ x + z, data = d, family = "binomial") predict(m, d %>% mutate(z = 1), type = "response") - predict(m, d %>% mutate(z = 0), type = "response") } plot_hte(d, s_learner_lr, "S-Learner(ロジスティック回帰ベース)によるHTE")
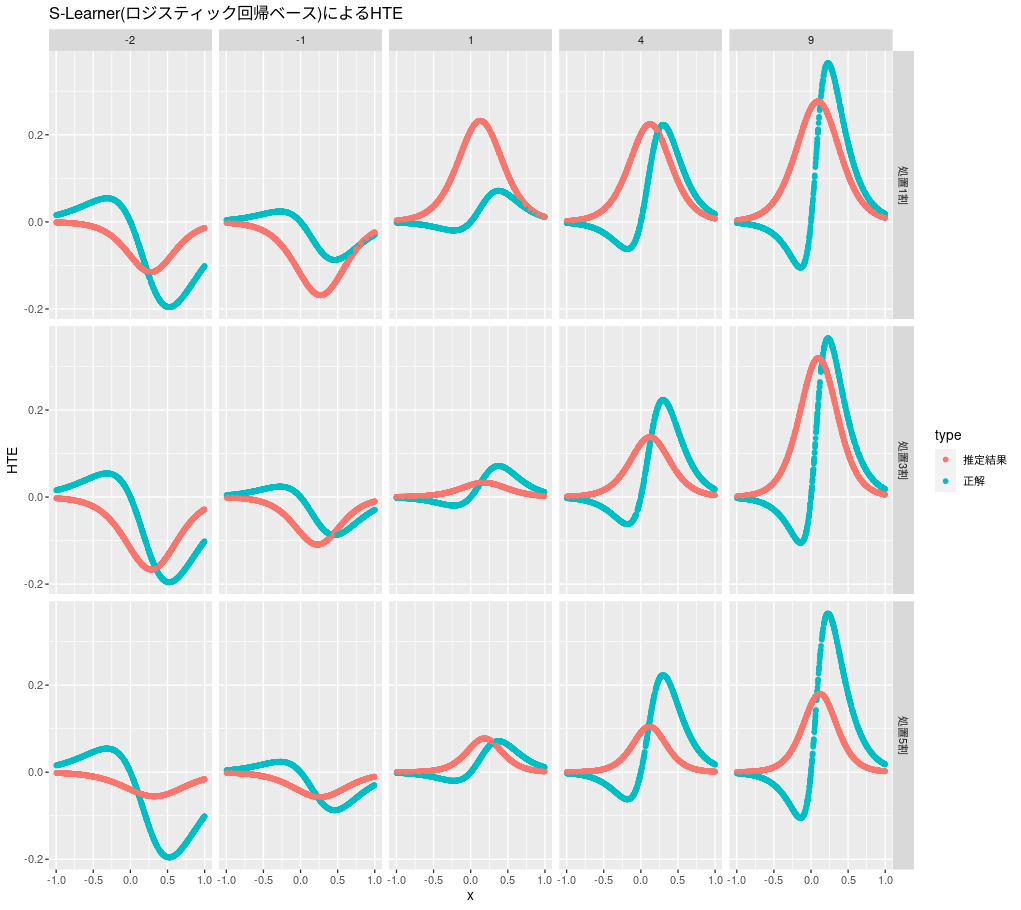
大きなピークはある程度捉えられているようですが、正負が反対のピークは捉えられていません。ロジスティック回帰ベースのS-Learnerでは、HTEを算出するモデル式の極値が一つしかないので2つのピークは表現できません。大きなピークのみを捉えるだけでよいケースでしか使えないので、利用用途が限られそうです。
比較用のランダムフォレストベースのS-Learnerの推定結果は次のようになります。アウトカムを2値として扱う方法と数値として扱う方法がありますが、今回のケースでは数値として扱った方がよい推定ができていたので、ここでは数値として扱っています。
s_learner_rf <- function(d) { m <- randomForest(y ~ x + z, data = d) predict(m, d %>% mutate(z = 1), type = "response") - predict(m, d %>% mutate(z = 0), type = "response") } plot_hte(d, s_learner_rf, "S-Learner(Randomforestベース)によるHTE")
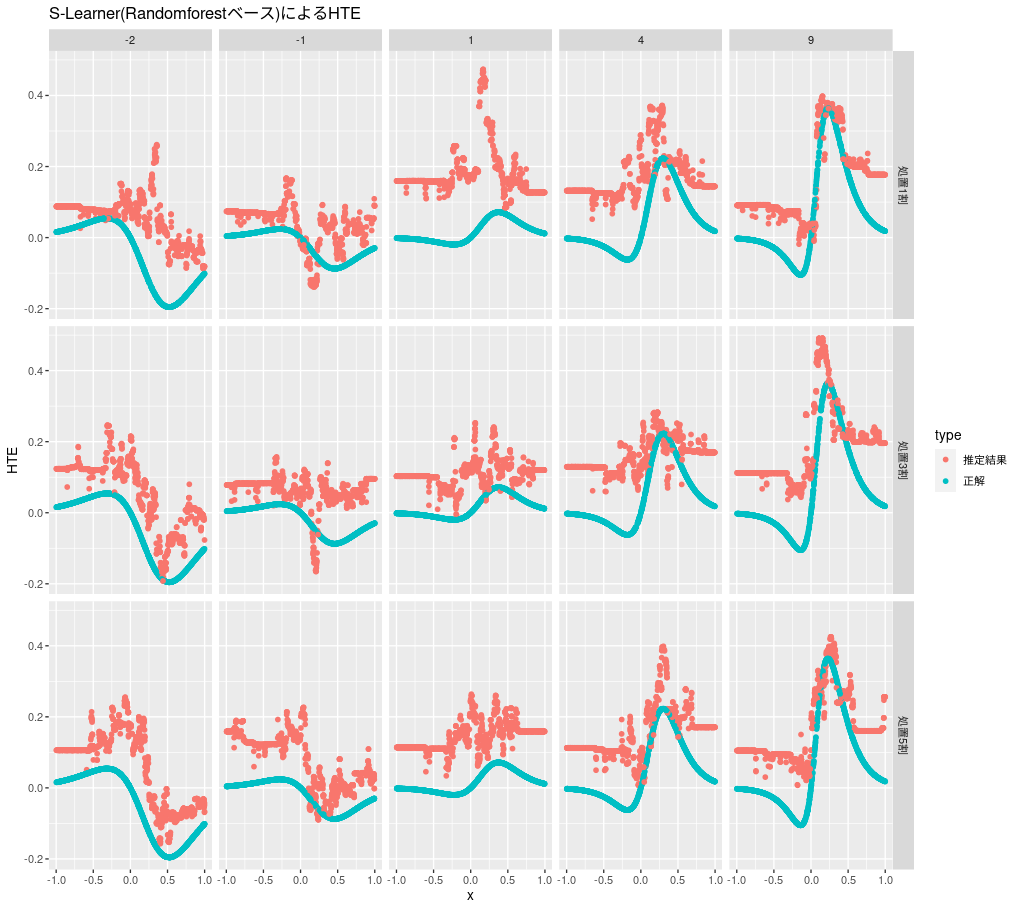
自由度が大きいのでぶれはあるものの、HTEのおおまかな形は捉えられており、特にHTEが大きいと処置比率が低めでもそれほど悪くはなさそうです。ただし、全般的に高めの推定値になっているので、効果を過大評価する懸念があります。
T-Learner
ロジスティック回帰ベースのT-Learnerの推定結果は次のようになります。
t_learner_lr <- function(d) { m0 <- glm(y ~ x, d %>% filter(z == 0), family = "binomial") m1 <- glm(y ~ x, d %>% filter(z == 1), family = "binomial") predict(m1, d, type = "response") - predict(m0, d, type = "response") } plot_hte(d, t_learner_lr, "T-Learner(ロジスティック回帰ベース)によるHTE")
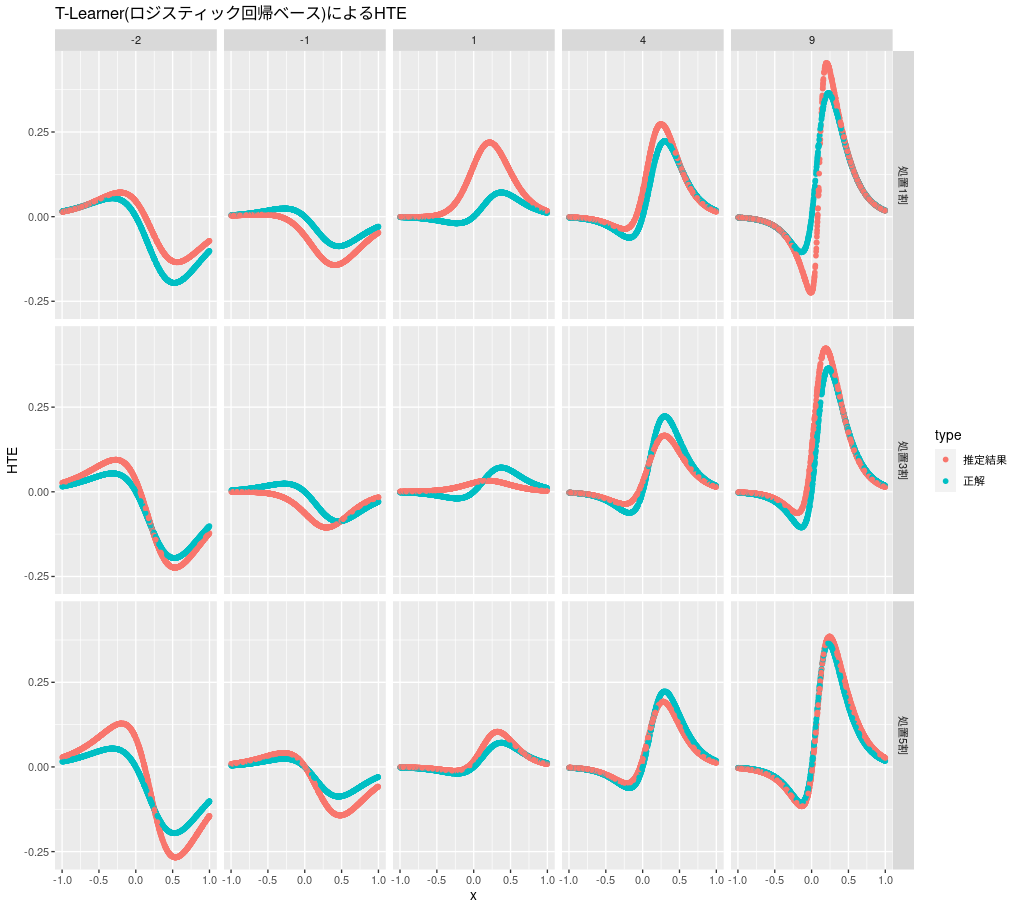
今回の問題設定ではよい推定ができているようです。おおむね効果が大きいほど、処置比率が5割に近いほどよい傾向が見られます。S-Learnerと異なり極値が一つではないので、HTEの2つのピークを表現できています。なお、今回推定対象となっているHTEはシグモイドの差で設定されており、ロジスティック回帰ベースのT-LearnerのHTE算出式と同じ形になっています。そのため他の方法と比較して推定がしやすくなっています。
比較用のランダムフォレストベースのT-Learnerの推定結果は次のようになります。こちらもアウトカムは数値として推定しています。
t_learner_rf <- function(d) { m0 <- randomForest(y ~ x, data = d %>% filter(z == 0)) m1 <- randomForest(y ~ x, data = d %>% filter(z == 1)) predict(m1, d, type = "response") - predict(m0, d, type = "response") } plot_hte(d, t_learner_rf, "T-Learner(Randomforestベース)によるHTE")
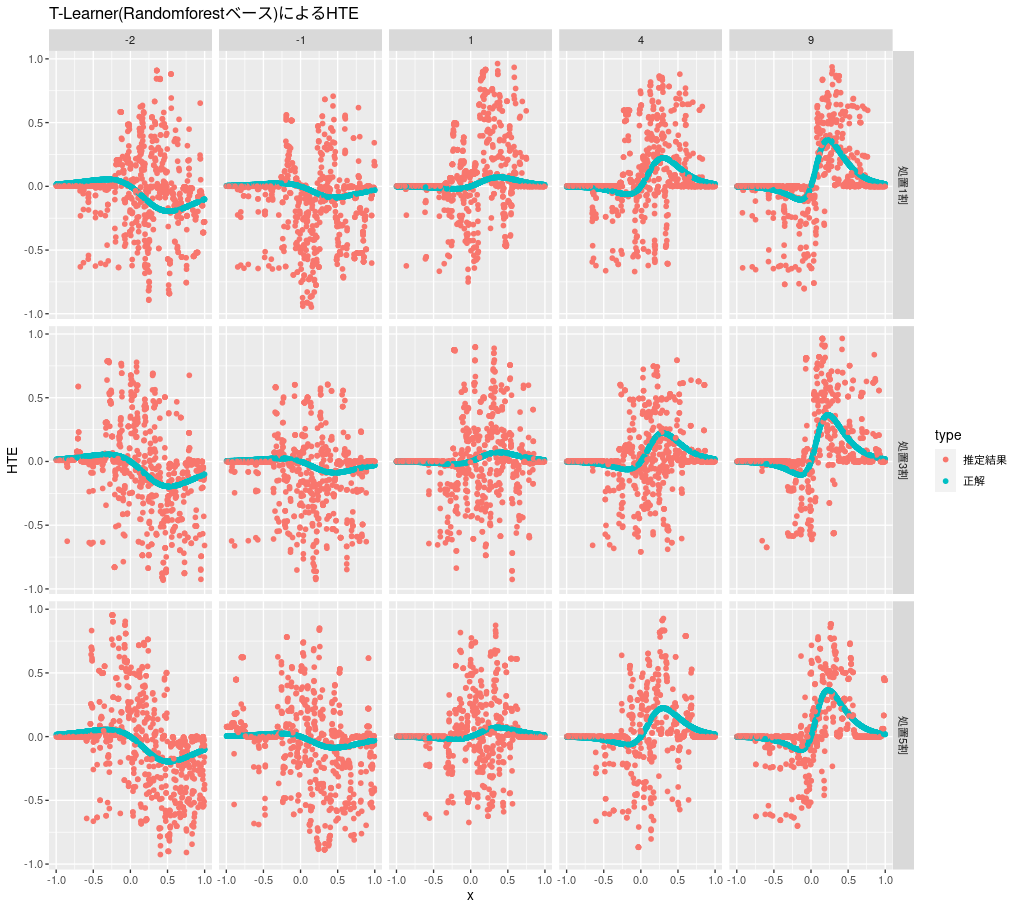
今回の問題設定ではうまくいかないようです。
X-Learner
X-Learnerでは、傾向スコアの計算のみロジスティック回帰を使い、他の部分ではランダムフォレストを使って実装します。imputed treatment effectsは2値でなく数値なのでロジスティック回帰で扱うことができないためこのような実装にしています。
x_learner <- function(d) { d0 <- d %>% filter(z == 0) d1 <- d %>% filter(z == 1) m0 <- randomForest(y ~ x, data = d0) m1 <- randomForest(y ~ x, data = d1) # imputed treatment effects D0 <- predict(m1, d0, type = "response") - d0$y D1 <- d1$y - predict(m0, d1, type = "response") m0_x <- randomForest(D0 ~ x, d0) m1_x <- randomForest(D1 ~ x, d1) g <- glm(z ~ x, d, family = "binomial") e <- predict(g, d, type = "response") e * predict(m0_x, d, type = "response") + (1 - e) * predict(m1_x, d, type = "response") } plot_hte(d, x_learner, "X-Learner(Randomforestベース)によるHTE")
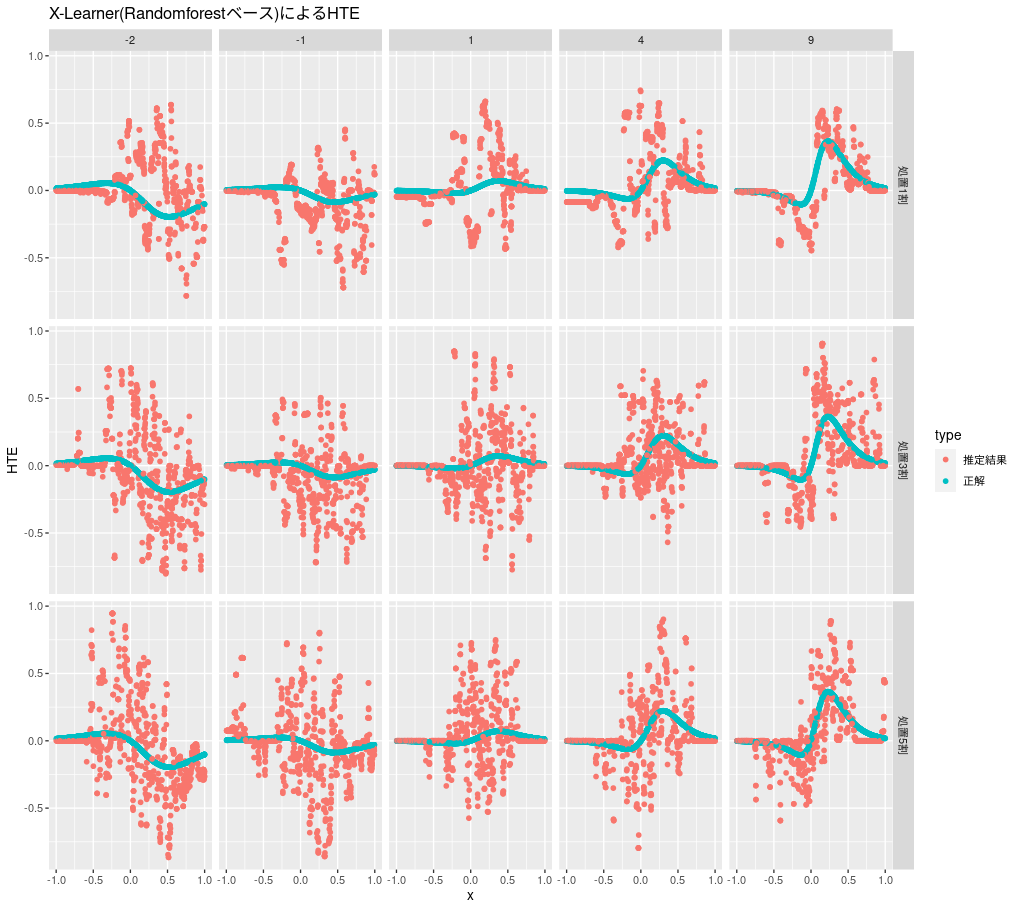
今回のケースでは、T-Learnerよりはよいですが全般的にぶれが大きいようです。
GRF
GRFの推定結果は次のようになります。
grf_wrapper <- function(d) { tau.forest <- causal_forest(X = as.matrix(d$x), Y = d$y, W = d$z) predict(tau.forest)$predictions } plot_hte(d, grf_wrapper, "GRFによるHTE")
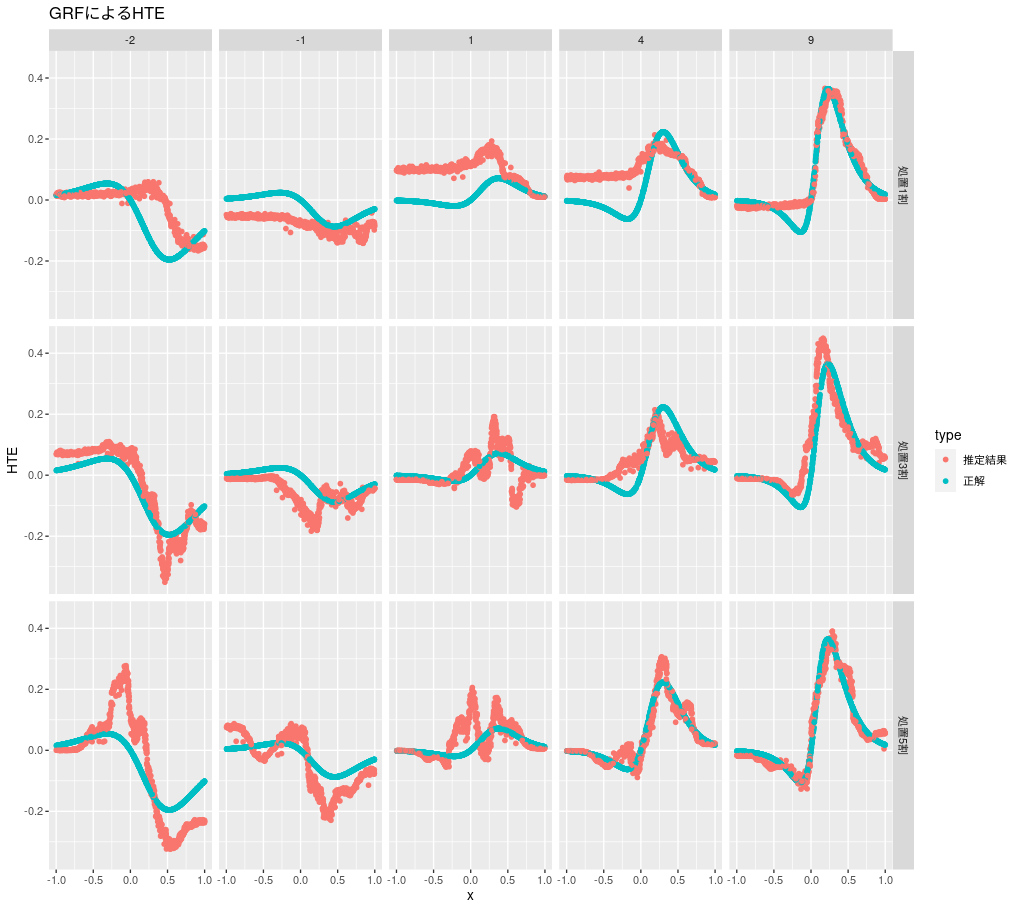
効果が大きいときはうまく推定できてそうですが、小さくなると難しいようです。
まとめ
今回はアウトカムが2値のHTEに関する簡単な検証実験を行いました。HTEがシグモイドの差となる単純なケースで効果が大きく処置比率も5割に近い場合は、ロジスティック回帰ベースのT-Learnerでよく推定できることを確認できました。また、パラメトリックなモデルのみを使ってHTEを推定しようとすると、実質的に利用できそうな手法がロジスティック回帰ベースのT-Learnerのみであることもわかりました。
